Slope Worksheet Review for Math Students
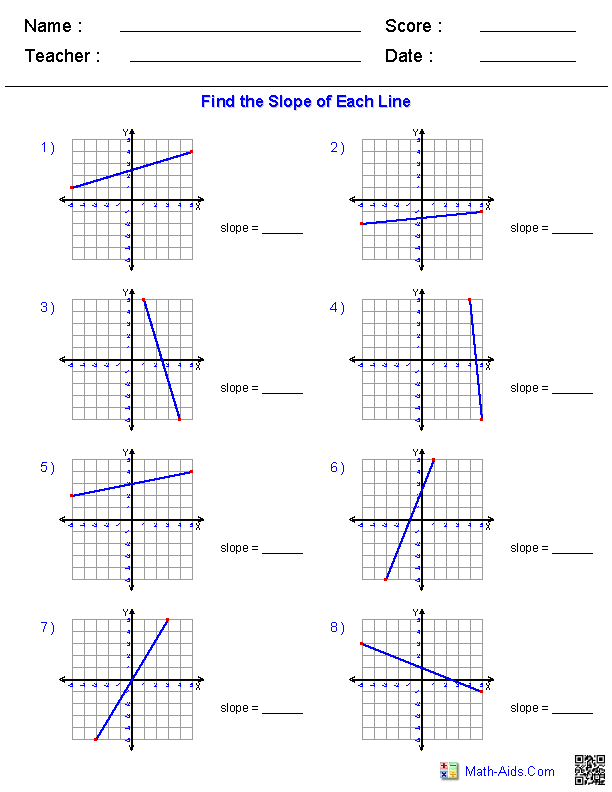
Understanding Slope in Mathematics
Slope is a fundamental concept in mathematics, particularly in algebra and geometry. It represents the measure of how much a line rises (or falls) vertically over a given horizontal distance. Understanding slope is crucial for graphing lines, solving linear equations, and modeling real-world phenomena. In this article, we will review the basics of slope, its types, and provide examples to help math students grasp this concept.
What is Slope?
The slope of a line is defined as the ratio of the vertical change (rise) to the horizontal change (run) between two points on the line. It can be calculated using the slope formula:
Slope (m) = (y2 - y1) / (x2 - x1)
where (x1, y1) and (x2, y2) are two points on the line.
Types of Slope
There are several types of slope, including:
- Positive Slope: A line with a positive slope rises from left to right.
- Negative Slope: A line with a negative slope falls from left to right.
- Zero Slope: A line with a zero slope is horizontal and does not rise or fall.
- Undefined Slope: A line with an undefined slope is vertical and does not have a defined horizontal change.
Calculating Slope
To calculate the slope of a line, follow these steps:
- Choose two points on the line.
- Label the points as (x1, y1) and (x2, y2).
- Calculate the vertical change (rise) by subtracting y1 from y2.
- Calculate the horizontal change (run) by subtracting x1 from x2.
- Divide the rise by the run to get the slope.
Example:
Find the slope of the line passing through points (2, 3) and (4, 5).
m = (5 - 3) / (4 - 2) = 2 / 2 = 1
The slope of the line is 1.
Real-World Applications of Slope
Slope has numerous real-world applications, including:
- Physics: Slope is used to describe the steepness of a ramp or an inclined plane.
- Engineering: Slope is used to design roads, bridges, and buildings.
- Economics: Slope is used to model supply and demand curves.
Slope Worksheet Review
To reinforce your understanding of slope, try the following worksheet:
| Problem | Solution |
|---|---|
| Find the slope of the line passing through points (1, 2) and (3, 4). | m = (4 - 2) / (3 - 1) = 2 / 2 = 1 |
| Find the slope of the line passing through points (2, 3) and (4, 6). | m = (6 - 3) / (4 - 2) = 3 / 2 = 1.5 |
| Find the slope of the line passing through points (3, 4) and (5, 6). | m = (6 - 4) / (5 - 3) = 2 / 2 = 1 |
📝 Note: You can use online tools or graphing calculators to verify your answers.
Conclusion
Understanding slope is essential for math students to grasp various concepts in algebra and geometry. By mastering the slope formula and practicing with worksheets, you can develop a deeper understanding of this fundamental concept. Remember to apply slope to real-world scenarios to appreciate its significance.
What is the difference between positive and negative slope?
+A positive slope indicates a line that rises from left to right, while a negative slope indicates a line that falls from left to right.
How do I calculate the slope of a line given two points?
+Use the slope formula: m = (y2 - y1) / (x2 - x1), where (x1, y1) and (x2, y2) are the two points on the line.
What is the significance of slope in real-world applications?
+Slope is used to describe the steepness of a ramp or an inclined plane, design roads and buildings, and model supply and demand curves in economics.