5 Ways to Find Triangular Prism Surface Area
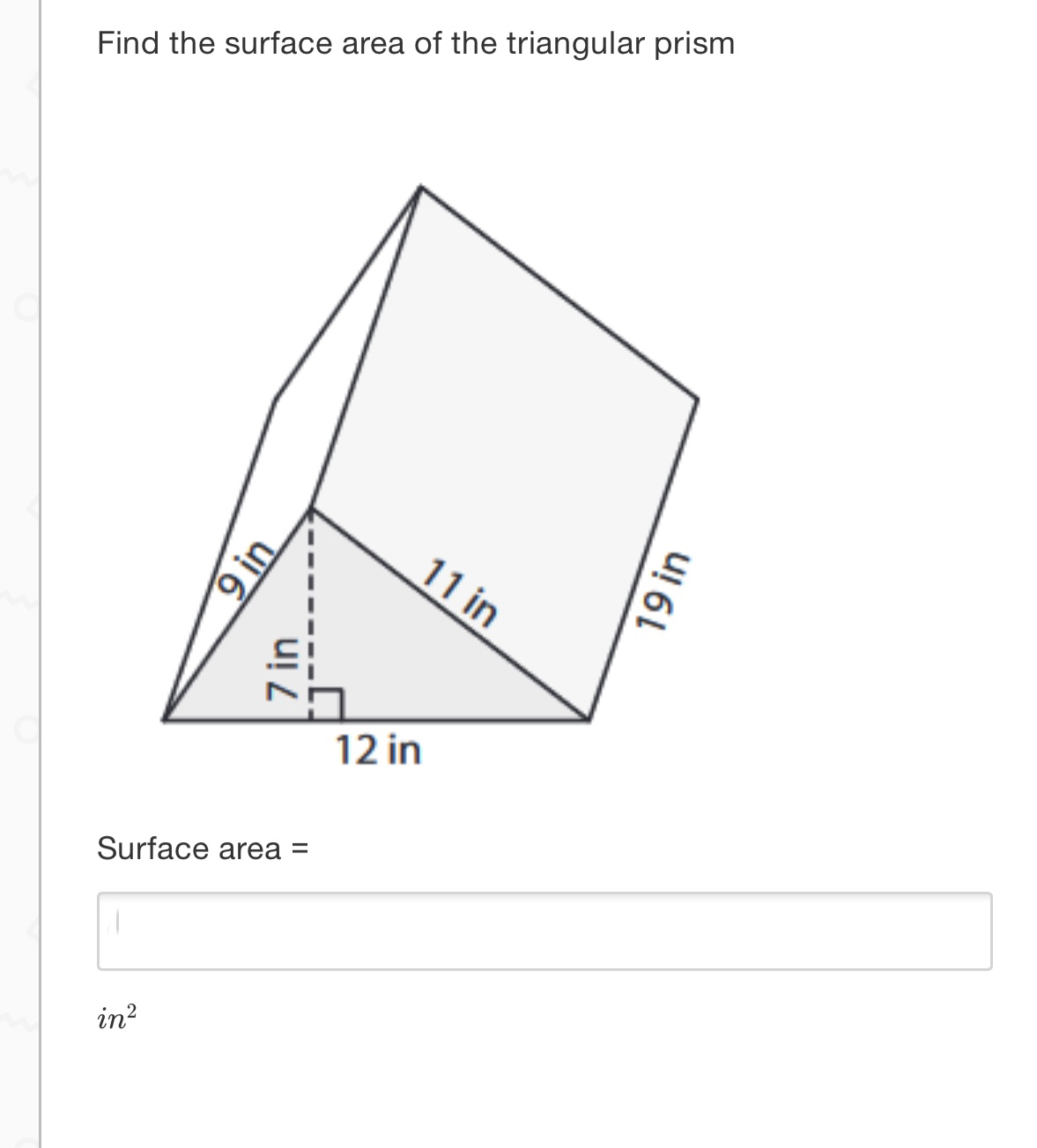
Understanding Triangular Prisms and Their Surface Area
A triangular prism is a three-dimensional shape with two identical faces that are triangles, and three rectangular faces connecting them. The surface area of a triangular prism can be calculated by finding the sum of the areas of all its faces. In this article, we will explore five different methods to calculate the surface area of a triangular prism.
Method 1: Using the Formula
The most straightforward way to calculate the surface area of a triangular prism is by using the formula:
Surface Area = 2 × (Base Area) + (Perimeter of Base × Height)
Where:
- Base Area is the area of one of the triangular faces
- Perimeter of Base is the sum of the lengths of the sides of the triangular face
- Height is the distance between the two triangular faces
This formula can be applied to any triangular prism, regardless of its size or shape.
Example:
Suppose we have a triangular prism with a base area of 12 square units, a perimeter of 12 units, and a height of 5 units. Using the formula, we can calculate the surface area as follows:
Surface Area = 2 × (12) + (12 × 5) Surface Area = 24 + 60 Surface Area = 84 square units
📝 Note: Make sure to plug in the correct values for base area, perimeter, and height to get the accurate surface area.
Method 2: Breaking Down the Prism into Faces
Another way to calculate the surface area of a triangular prism is to break it down into its individual faces. A triangular prism has five faces: two triangular faces and three rectangular faces.
- The two triangular faces have the same area, which can be calculated using the formula for the area of a triangle: (Base × Height) / 2
- The three rectangular faces have areas equal to the product of their length and width
By adding up the areas of all five faces, we can find the total surface area of the prism.
Example:
Suppose we have a triangular prism with two triangular faces with base lengths of 6 units and heights of 4 units. The three rectangular faces have dimensions of 6 units × 5 units, 4 units × 5 units, and 6 units × 4 units.
Using the formula for the area of a triangle, we can calculate the area of one triangular face:
Area of Triangular Face = (6 × 4) / 2 Area of Triangular Face = 12 square units
Since the two triangular faces have the same area, we can multiply this value by 2:
Total Area of Triangular Faces = 2 × 12 Total Area of Triangular Faces = 24 square units
The areas of the three rectangular faces are:
Area of Rectangular Face 1 = 6 × 5 Area of Rectangular Face 1 = 30 square units
Area of Rectangular Face 2 = 4 × 5 Area of Rectangular Face 2 = 20 square units
Area of Rectangular Face 3 = 6 × 4 Area of Rectangular Face 3 = 24 square units
Adding up the areas of all five faces, we get:
Total Surface Area = 24 + 30 + 20 + 24 Total Surface Area = 98 square units
📝 Note: Make sure to calculate the areas of all five faces correctly to get the accurate surface area.
Method 3: Using the Net of the Prism
A net is a two-dimensional representation of a three-dimensional shape. The net of a triangular prism consists of five rectangles: two identical rectangles that form the triangular faces, and three rectangles that form the rectangular faces.
By calculating the area of each rectangle and adding them up, we can find the total surface area of the prism.
Example:
Suppose we have a triangular prism with a net consisting of five rectangles:
- Two identical rectangles with dimensions of 6 units × 4 units
- Three rectangles with dimensions of 6 units × 5 units, 4 units × 5 units, and 6 units × 4 units
The areas of the two triangular faces are:
Area of Triangular Face = 6 × 4 Area of Triangular Face = 24 square units
Since the two triangular faces have the same area, we can multiply this value by 2:
Total Area of Triangular Faces = 2 × 24 Total Area of Triangular Faces = 48 square units
The areas of the three rectangular faces are:
Area of Rectangular Face 1 = 6 × 5 Area of Rectangular Face 1 = 30 square units
Area of Rectangular Face 2 = 4 × 5 Area of Rectangular Face 2 = 20 square units
Area of Rectangular Face 3 = 6 × 4 Area of Rectangular Face 3 = 24 square units
Adding up the areas of all five rectangles, we get:
Total Surface Area = 48 + 30 + 20 + 24 Total Surface Area = 122 square units
📝 Note: Make sure to calculate the areas of all five rectangles correctly to get the accurate surface area.
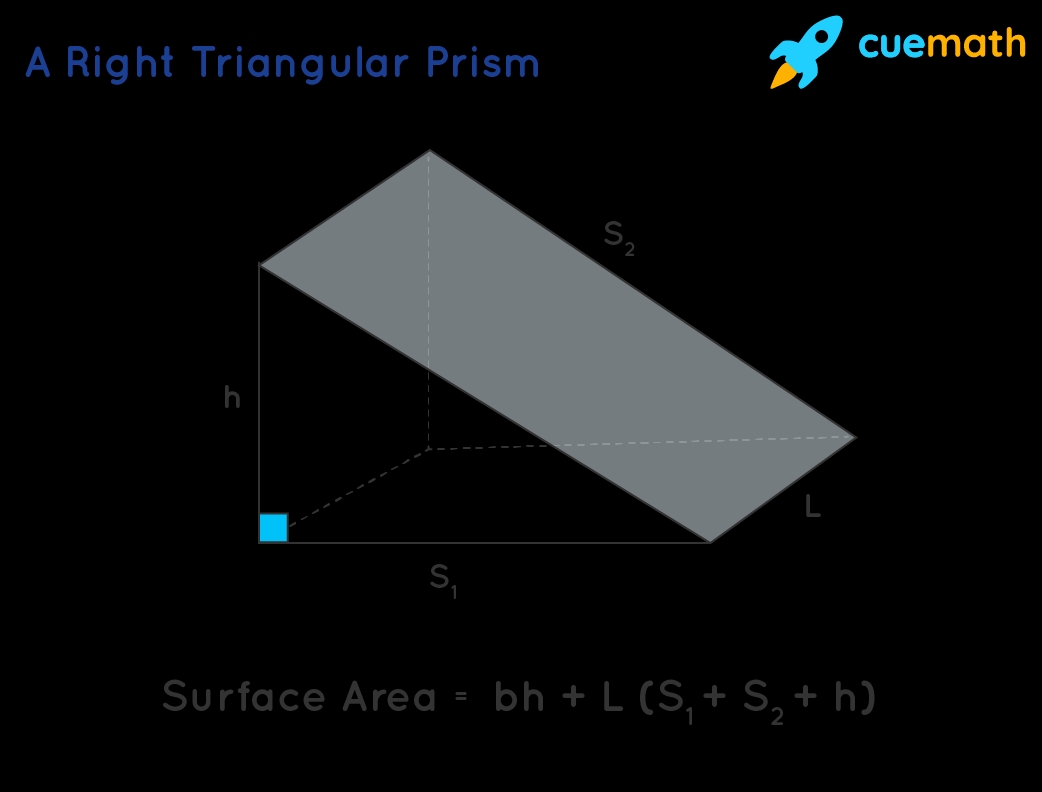
Method 4: Using the Dimensions of the Prism
If we know the dimensions of the triangular prism, we can calculate the surface area using the formula:
Surface Area = 2 × (Base × Height) + (Perimeter of Base × Height)
Where:
- Base is the length of one side of the triangular face
- Height is the distance between the two triangular faces
- Perimeter of Base is the sum of the lengths of the sides of the triangular face
Example:
Suppose we have a triangular prism with a base length of 6 units, a height of 5 units, and a perimeter of 12 units.
Using the formula, we can calculate the surface area as follows:
Surface Area = 2 × (6 × 5) + (12 × 5) Surface Area = 60 + 60 Surface Area = 120 square units
📝 Note: Make sure to plug in the correct values for base, height, and perimeter to get the accurate surface area.
Method 5: Using a Table or Chart
Another way to calculate the surface area of a triangular prism is to use a table or chart. We can create a table with the dimensions of the prism and calculate the surface area using the formula.
| Base Length | Height | Perimeter of Base | Surface Area |
|---|---|---|---|
| 6 units | 5 units | 12 units | 120 square units |
By using a table or chart, we can quickly calculate the surface area of a triangular prism without having to perform complex calculations.
📝 Note: Make sure to create the table or chart correctly to get the accurate surface area.
To summarize, there are five ways to calculate the surface area of a triangular prism: using the formula, breaking down the prism into faces, using the net of the prism, using the dimensions of the prism, and using a table or chart. Each method has its own advantages and disadvantages, and the choice of method depends on the specific problem and the information given.
What is the formula for the surface area of a triangular prism?
+
The formula for the surface area of a triangular prism is: Surface Area = 2 × (Base Area) + (Perimeter of Base × Height)
How do I calculate the surface area of a triangular prism using the net?
+
To calculate the surface area of a triangular prism using the net, calculate the area of each rectangle and add them up.
What are the five methods to calculate the surface area of a triangular prism?
+
The five methods to calculate the surface area of a triangular prism are: using the formula, breaking down the prism into faces, using the net of the prism, using the dimensions of the prism, and using a table or chart.



