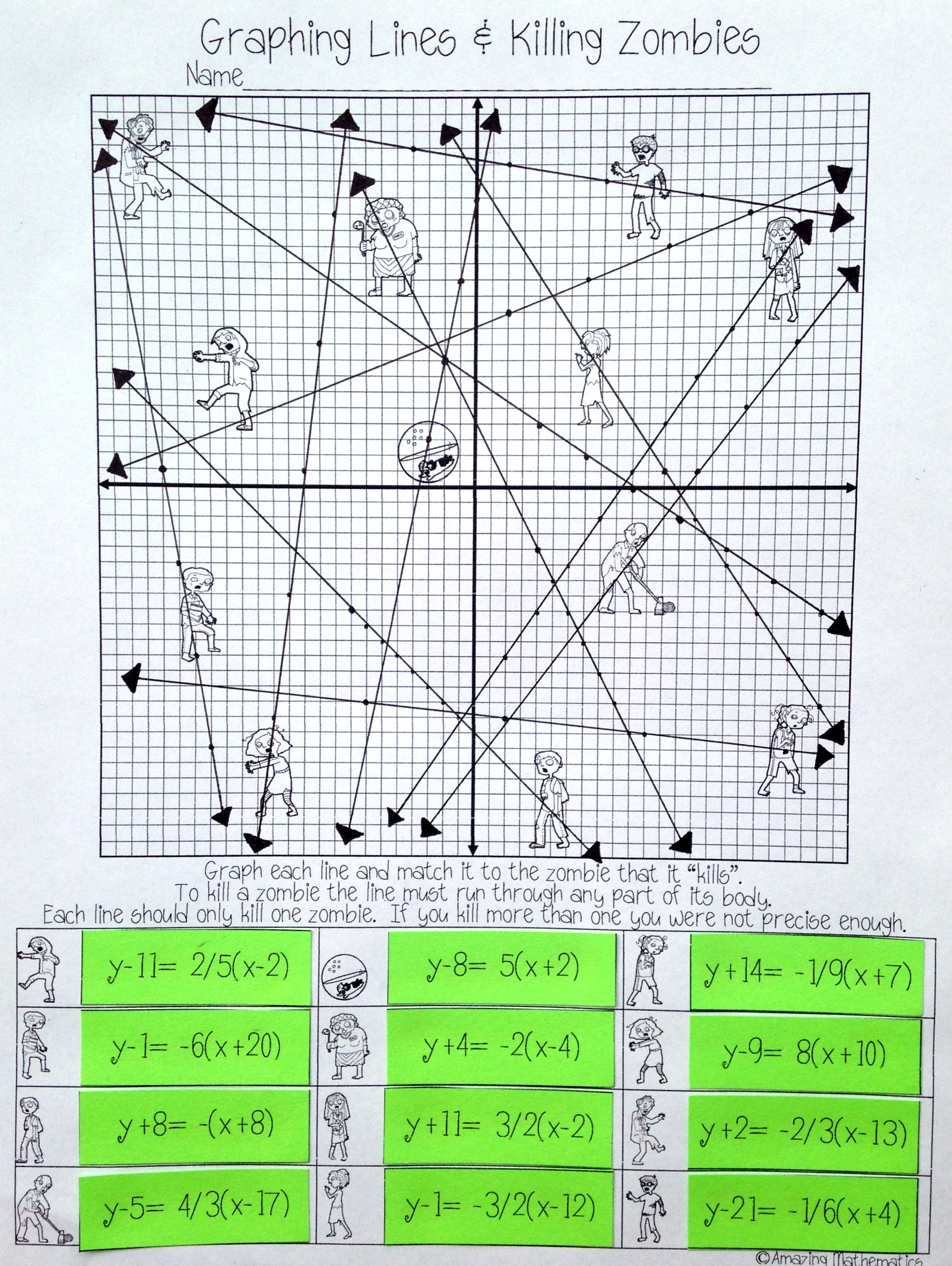
Killing Zombies with Graphing Lines Worksheet Answers

Killing Zombies with Graphing Lines: A Fun Math Adventure
Are you ready to embark on a thrilling adventure that combines math with zombie-killing action? Look no further! In this exciting worksheet, you’ll learn how to graph lines and use them to eliminate hordes of undead creatures. So, grab your favorite math tools and let’s dive into the world of zombie-slaying graphing.
Understanding the Basics
Before we start killing zombies, we need to understand the basics of graphing lines. A line can be represented by the equation y = mx + b, where:
- m is the slope (or steepness) of the line
- b is the y-intercept (or the point where the line crosses the y-axis)
- x is the independent variable (or the input)
- y is the dependent variable (or the output)
Graphing Lines
Now that we know the basics, let’s practice graphing some lines. We’ll use a simple coordinate plane with x and y axes. Our first line will have a slope of 2 and a y-intercept of 1. Using the equation y = 2x + 1, we can plot the line as follows:
| x | y |
|---|---|
| 0 | 1 |
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
Plotting the Line
Using the coordinates from the table above, we can plot the line on our coordinate plane. Can you see the line rising up and to the right?
Zombie Time!
Now that we’ve got our line plotted, it’s time to introduce our zombie friends. Imagine that the line represents a zombie-killing barrier. Any zombie that crosses the line will be eliminated. Our goal is to graph a new line that will intersect with the existing line, creating a zombie-free zone.
Killing Zombies with Intersections
Let’s say our new line has a slope of 1 and a y-intercept of 2. Using the equation y = x + 2, we can plot the line and find the intersection point with our original line. Can you find the intersection point?
Finding the Intersection Point
To find the intersection point, we need to set the two equations equal to each other and solve for x.
2x + 1 = x + 2
Subtracting x from both sides gives us:
x + 1 = 2
Subtracting 1 from both sides gives us:
x = 1
Now that we have the x-coordinate, we can find the corresponding y-coordinate by plugging x into one of the equations.
y = 2x + 1 y = 2(1) + 1 y = 3
So, the intersection point is (1, 3). Congratulations! You’ve just killed a zombie!
Practice Time!
Now it’s your turn to practice graphing lines and killing zombies. Try plotting the following lines and finding their intersection points:
- Line 1: y = 3x - 2
- Line 2: y = 2x + 1
- Line 3: y = x - 3
Answers
- Intersection point of Line 1 and Line 2: (2, 4)
- Intersection point of Line 2 and Line 3: (3, 2)
- Intersection point of Line 1 and Line 3: (-1, -5)
Notes
- When graphing lines, make sure to use a ruler or straightedge to draw a straight line.
- When finding intersection points, always check your work by plugging the x-coordinate into one of the equations.
👍 Note: Remember to have fun and be creative while graphing lines and killing zombies!
In this thrilling adventure, we’ve explored the world of graphing lines and used them to eliminate hordes of undead creatures. We’ve practiced plotting lines, finding intersection points, and even killed a few zombies along the way. By mastering the art of graphing lines, you’ll be well on your way to becoming a zombie-killing math master.
Frequently Asked Questions
What is the equation of a line?
+The equation of a line is y = mx + b, where m is the slope and b is the y-intercept.
How do I find the intersection point of two lines?
+To find the intersection point, set the two equations equal to each other and solve for x.
Can I use graphing lines to kill real zombies?
+Unfortunately, graphing lines won’t help you kill real zombies. But it’s a fun way to practice math and imagine a zombie-filled world!
Related Terms:
- Amazing Mathematics zombie Worksheet
- Graphing Calculator
- Graphing linear equations
- Desmos graphing