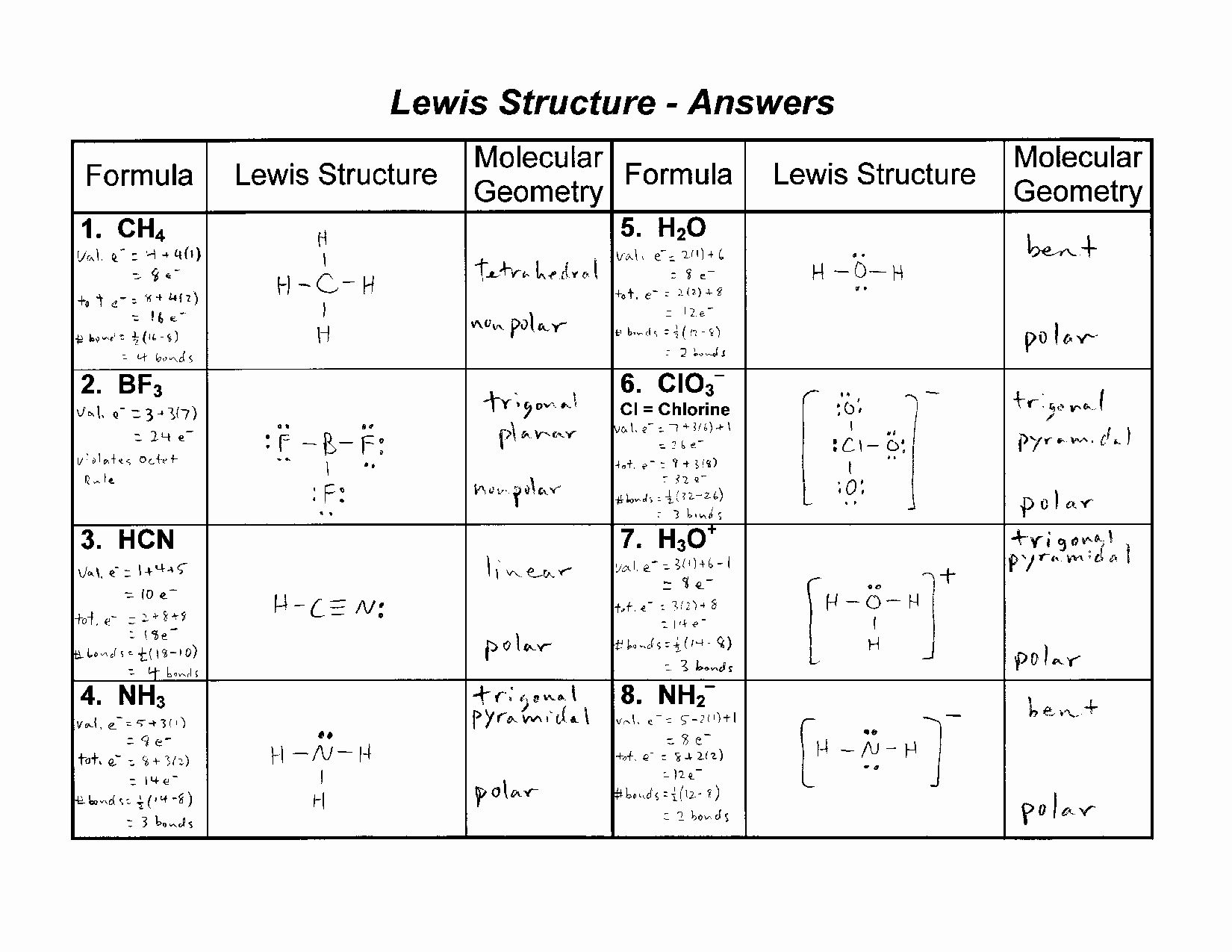
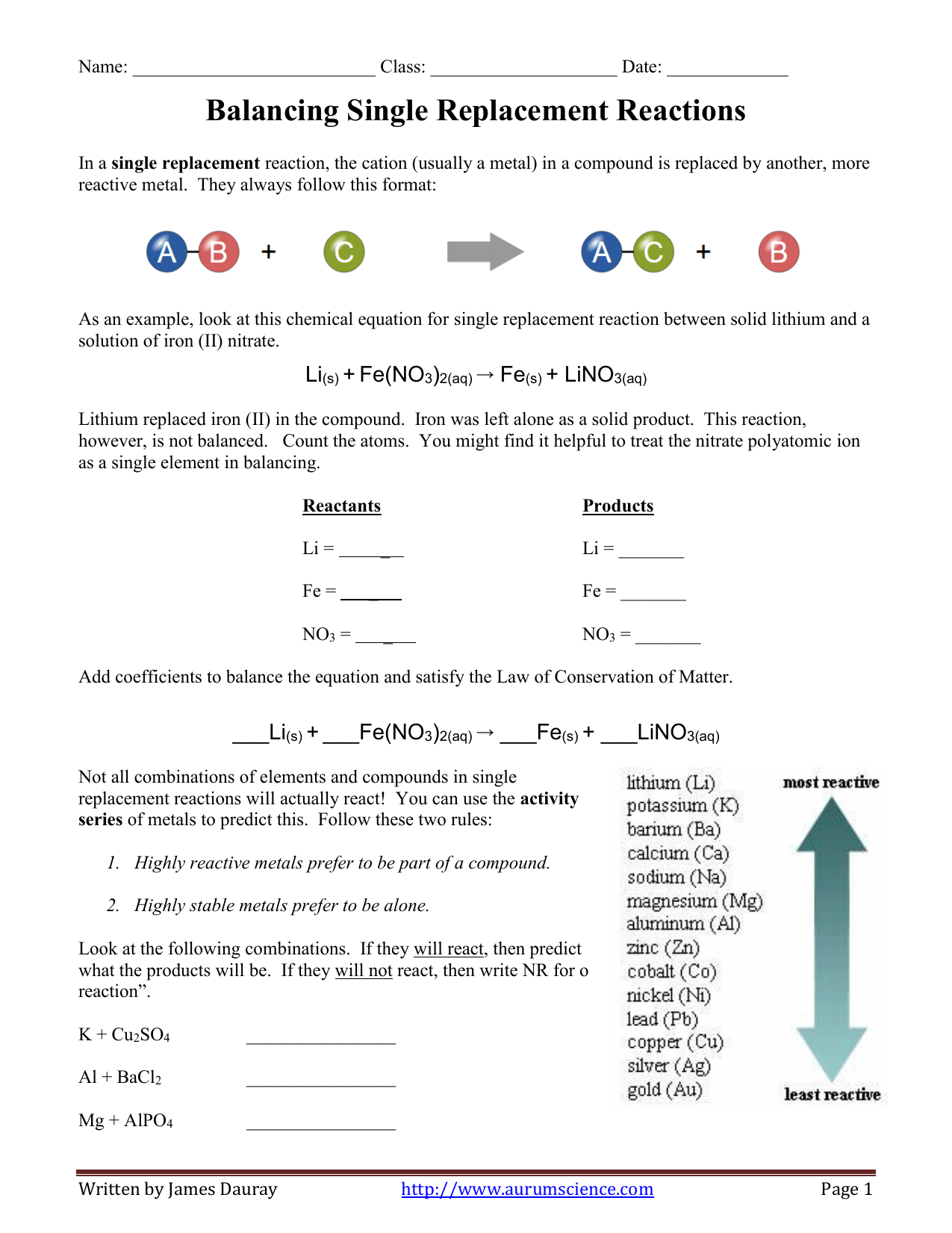
7Th Grade Proportional Relationships Worksheet
Understanding Proportional Relationships in 7th Grade Math
As students progress to 7th grade, they build on their understanding of ratios and proportions, delving deeper into proportional relationships. This concept is fundamental in mathematics and appears in various real-world applications, from science and engineering to finance and beyond. Here, we’ll explore what proportional relationships are, how to identify them, and how to solve problems involving these relationships.
What are Proportional Relationships?
A proportional relationship is a relationship between two quantities where a constant ratio exists between them. In other words, as one quantity increases or decreases, the other quantity does so in a predictable, consistent manner. This can be represented by the equation y = kx, where y is the dependent variable, x is the independent variable, and k is the constant of proportionality.
Identifying Proportional Relationships
To identify a proportional relationship, you can use several strategies:
- Graphical Method: Plotting the data on a coordinate plane. If the graph is a straight line passing through the origin (0,0), then the relationship is likely proportional.
- Table Method: Looking at a table of values. If you find a constant ratio between the two quantities, it suggests a proportional relationship.
- Equation Method: Examining the equation of the relationship. If it’s in the form y = kx, then it’s proportional.
Solving Problems Involving Proportional Relationships
Solving problems involving proportional relationships often requires finding the constant of proportionality (k) and using it to calculate unknown values.
Example Problem:
Tom is saving money for a new bike and has a part-time job that pays $8 per hour. If he saves all his earnings, how much will he have saved after working for 5 hours?
Solution:
Given that Tom earns $8 per hour, the relationship between his earnings (y) and the number of hours he works (x) is proportional. The constant of proportionality (k) is 8.
Using the equation y = kx, substitute k with 8 and x with 5 to find y:
y = 8 * 5 y = 40
Therefore, after working for 5 hours, Tom will have saved $40.
📝 Note: In real-world scenarios, you might encounter problems where the constant of proportionality is not immediately apparent. In such cases, you'll need to use the given data to find the value of k before solving for unknowns.
Applying Proportional Relationships to Real-Life Scenarios
Proportional relationships are ubiquitous in real life, appearing in:
- Science: Chemical reactions, where the amount of reactants is proportional to the amount of products.
- Finance: Interest on savings accounts, where the interest earned is proportional to the amount saved.
- Cooking: Recipes, where the amount of ingredients is proportional to the number of servings.
Understanding and applying proportional relationships in these contexts can help you make informed decisions, predict outcomes, and optimize processes.
Common Misconceptions and Challenges
Some common misconceptions when dealing with proportional relationships include:
- Assuming that all linear relationships are proportional. While all proportional relationships are linear, not all linear relationships are proportional.
- Forgetting to check if the relationship passes through the origin (0,0), which is a characteristic of proportional relationships.
To overcome these challenges, always verify the nature of the relationship through graphical, table, or equation analysis.
Practice Problems
Here are a few practice problems to help solidify your understanding of proportional relationships:
- Graphical Analysis: Given the graph below, determine if the relationship is proportional. If so, find the constant of proportionality.
| x | y |
|---|---|
| 2 | 6 |
| 4 | 12 |
| 6 | 18 |
- Table Analysis: A bakery sells a total of 250 loaves of bread per day. They offer a discount for bulk purchases, where the price per loaf decreases as the number of loaves increases. Use the table below to find the constant of proportionality between the number of loaves and the total price.
| Number of Loaves | Total Price ($) |
|---|---|
| 50 | 150 |
| 100 | 250 |
| 150 | 375 |
- Equation Analysis: Given the equation y = 2.5x, determine if the relationship is proportional. If so, find the value of y when x is 4.
Solutions to these problems can be found by applying the concepts discussed above.
What is the difference between a proportional relationship and a linear relationship?
+A proportional relationship is a specific type of linear relationship where the constant of proportionality is the same as the slope of the line, and the line passes through the origin (0,0). All proportional relationships are linear, but not all linear relationships are proportional.
How do I know if a relationship is proportional?
+You can determine if a relationship is proportional by analyzing the graph, table, or equation. Look for a constant ratio between the two quantities, and verify that the relationship passes through the origin (0,0).
What are some real-world applications of proportional relationships?
+Proportional relationships appear in various real-world contexts, including science, finance, cooking, and more. Understanding these relationships can help you make informed decisions, predict outcomes, and optimize processes.
In conclusion, proportional relationships are a fundamental concept in mathematics, and understanding them is crucial for solving problems in various fields. By identifying the constant of proportionality and applying it to real-world scenarios, you can develop a deeper appreciation for the intricacies of proportional relationships and improve your problem-solving skills.
Related Terms:
- Teacher synergy llc
- Khan Academy
- IXL
- BrainPOP
- Udacity
- Duolingo