Word Problems With Pythagorean Theorem Worksheet

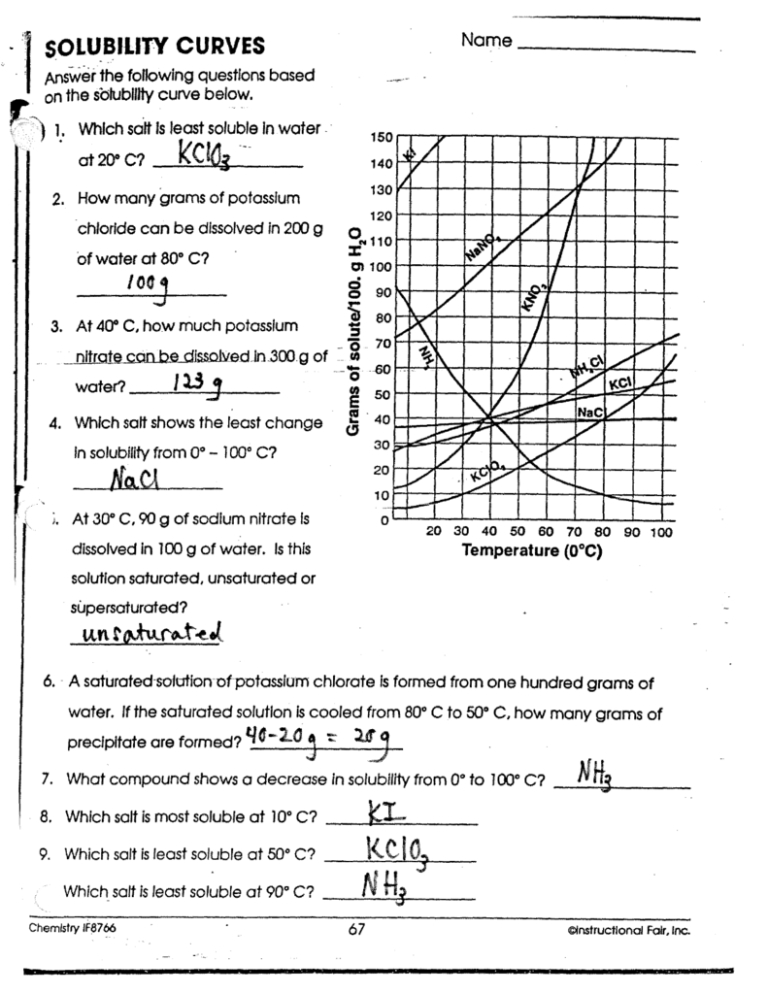
Understanding the Pythagorean Theorem
The Pythagorean Theorem is a fundamental concept in geometry that describes the relationship between the lengths of the sides of a right-angled triangle. The theorem states that the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This can be expressed mathematically as:
a² + b² = c²
where a and b are the lengths of the two sides that form the right angle, and c is the length of the hypotenuse.
Applying the Pythagorean Theorem to Word Problems
While the Pythagorean Theorem may seem like a abstract concept, it has many practical applications in real-world scenarios. Here are some examples of word problems that can be solved using the Pythagorean Theorem:
Example 1: Building Design
A architect is designing a new building with a triangular roof. The two sides of the roof that meet at the apex are 15 meters and 20 meters long. What is the length of the hypotenuse (the side opposite the apex)?
Solution:
Using the Pythagorean Theorem, we can calculate the length of the hypotenuse as follows:
a² + b² = c² 15² + 20² = c² 225 + 400 = c² 625 = c² c = √625 c = 25
Therefore, the length of the hypotenuse is 25 meters.
Example 2: Surveying
A surveyor is measuring the distance between two points on a map. She measures the horizontal distance to be 30 meters and the vertical distance to be 40 meters. What is the straight-line distance between the two points?
Solution:
Using the Pythagorean Theorem, we can calculate the straight-line distance as follows:
a² + b² = c² 30² + 40² = c² 900 + 1600 = c² 2500 = c² c = √2500 c = 50
Therefore, the straight-line distance between the two points is 50 meters.
Worksheet: Pythagorean Theorem Word Problems
Here are five word problems that you can solve using the Pythagorean Theorem:

| Problem | Description |
|---|---|
| 1 | A ladder is leaning against a wall. The ladder is 10 meters long, and the distance from the base of the ladder to the wall is 6 meters. What is the height of the ladder against the wall? |
| 2 | A park is in the shape of a right-angled triangle. The two sides of the park that meet at the right angle are 200 meters and 300 meters long. What is the length of the hypotenuse (the side opposite the right angle)? |
| 3 | A ship is sailing from one port to another. The distance between the two ports is 100 kilometers, and the ship is sailing at an angle of 60 degrees to the horizontal. What is the horizontal distance traveled by the ship? |
| 4 | A tree is leaning at an angle of 30 degrees to the horizontal. The distance from the base of the tree to the point where the tree meets the ground is 15 meters. What is the height of the tree? |
| 5 | A bridge is in the shape of a right-angled triangle. The two sides of the bridge that meet at the right angle are 50 meters and 70 meters long. What is the length of the hypotenuse (the side opposite the right angle)? |
Solutions:
- a² + b² = c² 6² + b² = 10² 36 + b² = 100 b² = 64 b = √64 b = 8
Therefore, the height of the ladder against the wall is 8 meters.
- a² + b² = c² 200² + 300² = c² 40000 + 90000 = c² 130000 = c² c = √130000 c = 360.56
Therefore, the length of the hypotenuse is approximately 360.56 meters.
- a² + b² = c² 100² + b² = c² 10000 + b² = c² b² = c² - 10000 b² = 10000tan²(60) b² = 40000 b = √40000 b = 200
Therefore, the horizontal distance traveled by the ship is 200 kilometers.
- a² + b² = c² 15² + b² = c² 225 + b² = c² b² = c² - 225 b² = 225tan²(30) b² = 100 b = √100 b = 10
Therefore, the height of the tree is 10 meters.
- a² + b² = c² 50² + 70² = c² 2500 + 4900 = c² 7400 = c² c = √7400 c = 86.03
Therefore, the length of the hypotenuse is approximately 86.03 meters.
📝 Note: These solutions assume that the angles and side lengths are exact, and do not take into account any real-world limitations or inaccuracies.
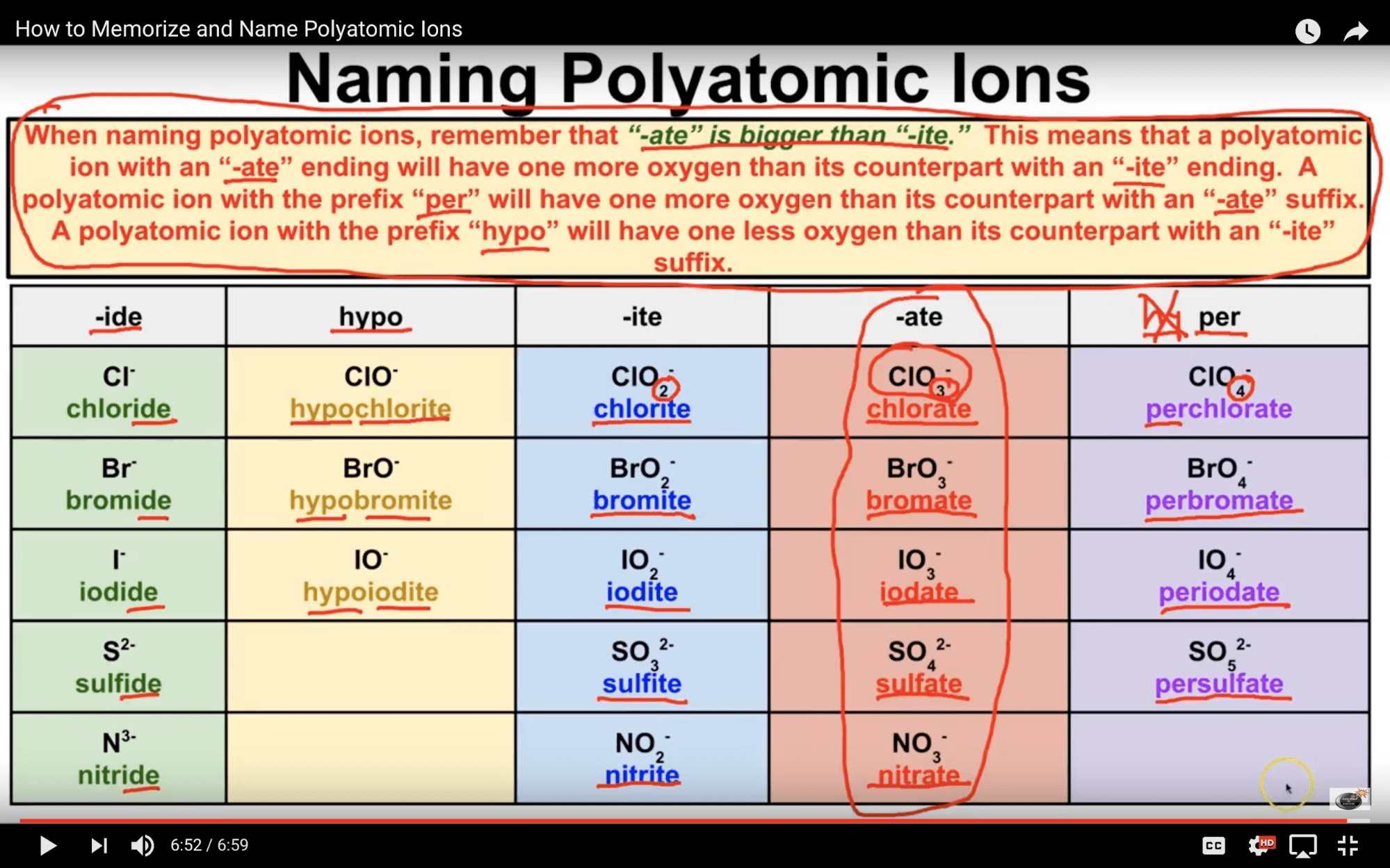
What is the Pythagorean Theorem?
+The Pythagorean Theorem is a mathematical concept that describes the relationship between the lengths of the sides of a right-angled triangle. It states that the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
How do I apply the Pythagorean Theorem to word problems?
+To apply the Pythagorean Theorem to word problems, you need to identify the lengths of the sides of the right-angled triangle and then use the formula a² + b² = c² to calculate the length of the hypotenuse. You can also use the theorem to find the length of one of the other sides, given the length of the hypotenuse and one of the other sides.
What are some real-world applications of the Pythagorean Theorem?
+The Pythagorean Theorem has many real-world applications, including building design, surveying, and physics. It can be used to calculate distances, heights, and lengths in a wide range of scenarios.
Related Terms:
- Pythagorean Word Problems Worksheet pdf