Trig Word Problems Worksheet Answers and Solutions

Trigonometry and Its Real-World Applications
Trigonometry is a branch of mathematics that deals with the relationships between the sides and angles of triangles. It has numerous applications in various fields such as physics, engineering, navigation, and computer science. Word problems involving trigonometry are used to test a student’s ability to apply mathematical concepts to real-world situations.
Types of Trig Word Problems
There are several types of trig word problems, including:
- Angle of Elevation: These problems involve finding the angle of elevation of an object above the horizon.
- Angle of Depression: These problems involve finding the angle of depression of an object below the horizon.
- Distance and Height: These problems involve finding the distance or height of an object using trigonometric ratios.
- Surveying: These problems involve using trigonometry to determine distances and angles between landmarks.
- Physics and Engineering: These problems involve using trigonometry to solve problems related to motion, forces, and energies.
How to Solve Trig Word Problems
To solve trig word problems, follow these steps:
- Read the problem carefully: Understand what is given and what is required to find.
- Draw a diagram: Draw a diagram to represent the situation and identify the relevant trigonometric relationships.
- Choose a trig ratio: Choose the appropriate trigonometric ratio (sine, cosine, or tangent) based on the information given.
- Plug in values: Plug in the given values into the trig ratio and solve for the unknown.
- Check the answer: Check the answer to ensure it is reasonable and makes sense in the context of the problem.
Example Problems
Here are some example problems and their solutions:
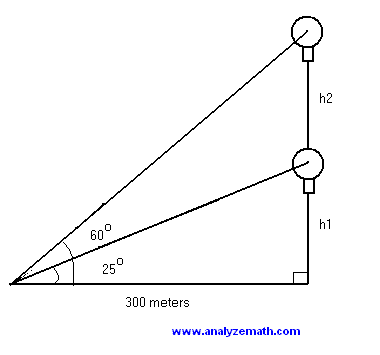
Example 1: Angle of Elevation
A surveyor is measuring the height of a building that is 50 meters away. If the angle of elevation to the top of the building is 60°, how tall is the building?
Solution: Use the tangent ratio to solve for the height.
tan(60°) = opposite / adjacent tan(60°) = height / 50 height = 50 × tan(60°) = 86.6 meters
Example 2: Distance and Height
A plane is flying at an altitude of 2000 meters. If the angle of depression to a point on the ground is 30°, how far is the plane from the point?
Solution: Use the tangent ratio to solve for the distance.
tan(30°) = opposite / adjacent tan(30°) = 2000 / distance distance = 2000 / tan(30°) = 3464.1 meters
Notes
📝 Note: When solving trig word problems, always check the units of measurement to ensure they are consistent.
📝 Note: Use a calculator to find the values of trigonometric ratios, but make sure to check the mode (degrees or radians) to ensure accuracy.
Table of Trig Ratios
| Trig Ratio | Formula |
|---|---|
| Sine (sin) | opposite / hypotenuse |
| Cosine (cos) | adjacent / hypotenuse |
| Tangent (tan) | opposite / adjacent |
Conclusion
Trigonometry is a powerful tool for solving problems in various fields. By understanding the concepts and relationships between trigonometric ratios, you can apply them to solve a wide range of word problems. Remember to always read the problem carefully, draw a diagram, and choose the appropriate trig ratio to solve for the unknown.
FAQ Section
What is the difference between angle of elevation and angle of depression?
+Angle of elevation is the angle above the horizon, while angle of depression is the angle below the horizon.
How do I choose the correct trig ratio to use in a word problem?
+Choose the trig ratio that involves the given information and the unknown value you want to find. For example, if you are given the opposite side and the hypotenuse, use the sine ratio.
Can I use a calculator to solve trig word problems?
+Yes, you can use a calculator to find the values of trigonometric ratios, but make sure to check the mode (degrees or radians) to ensure accuracy.