5 Ways to Factor Out the GCF

Understanding the Greatest Common Factor (GCF)

When working with algebraic expressions, factoring out the Greatest Common Factor (GCF) is a fundamental concept that helps simplify expressions and solve equations. The GCF is the largest factor that divides all the terms of an expression without leaving a remainder. Factoring out the GCF can make it easier to solve equations, simplify expressions, and identify patterns.

Method 1: Identify the GCF and Factor it Out

One way to factor out the GCF is to identify the largest factor that divides all the terms of the expression. This can be done by finding the prime factors of each term and identifying the common factors.

For example, consider the expression: 12x + 18y

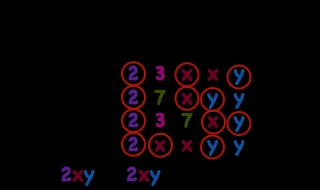
The prime factors of 12 are 2 x 2 x 3 The prime factors of 18 are 2 x 3 x 3

The GCF of 12 and 18 is 6, since 6 is the largest factor that divides both numbers.

Factoring out the GCF, we get: 6(2x + 3y)

Method 2: Use the Distributive Property

Another way to factor out the GCF is to use the distributive property, which states that a(b + c) = ab + ac.

For example, consider the expression: 4x^2 + 12x

We can factor out the GCF of 4 by using the distributive property:

4x^2 + 12x = 4(x^2 + 3x)

Method 3: Look for Common Bins

When factoring out the GCF, it’s essential to look for common bins, which are groups of terms that have a common factor.

For example, consider the expression: 2x^2 + 4x + 6x^2 + 12x

We can group the terms into common bins:

(2x^2 + 4x) + (6x^2 + 12x)

Factoring out the GCF from each bin, we get:

2x(x + 2) + 6x(x + 2)

Now, we can factor out the common bin (x + 2):

(2x + 6x)(x + 2)

Simplifying, we get:

8x(x + 2)

Method 4: Use the Factoring by Grouping Method

Factoring by grouping is a technique used to factor out the GCF from expressions that have four or more terms.

For example, consider the expression: x^2 + 2x + 3x + 6

We can group the terms into pairs:

(x^2 + 2x) + (3x + 6)

Factoring out the GCF from each pair, we get:

x(x + 2) + 3(x + 2)

Now, we can factor out the common bin (x + 2):

(x + 3)(x + 2)

Method 5: Use the GCF of the Coefficients

When factoring out the GCF, we can also look at the coefficients of the terms.

For example, consider the expression: 9x^2 + 12x

The GCF of the coefficients 9 and 12 is 3.

Factoring out the GCF, we get:

3(3x^2 + 4x)

📝 Note: When factoring out the GCF, always check to make sure that the resulting expression is equivalent to the original expression.

📝 Note: The GCF can be a single variable, a constant, or a combination of variables and constants.

In conclusion, factoring out the GCF is an essential skill in algebra that can help simplify expressions, solve equations, and identify patterns. By using the methods outlined above, you can develop a strong understanding of how to factor out the GCF and become proficient in algebra.