6 Ways to Master Midpoint and Distance Calculations

Introduction to Midpoint and Distance Calculations
In mathematics, particularly in geometry and trigonometry, calculating midpoints and distances is crucial for solving problems involving points, lines, and shapes on the coordinate plane. These calculations are used extensively in various fields such as physics, engineering, architecture, and more. This blog post will guide you through six ways to master midpoint and distance calculations, providing you with a comprehensive understanding of these concepts and their applications.
Understanding Midpoints
A midpoint is a point that divides a line segment into two equal parts. It is essential to understand how to calculate the midpoint of a line segment, as it is a fundamental concept in geometry and trigonometry. The formula to calculate the midpoint of a line segment with endpoints (x1, y1) and (x2, y2) is:
M = ((x1 + x2) / 2, (y1 + y2) / 2)
where M is the midpoint of the line segment.
Example: Calculating the Midpoint
Find the midpoint of the line segment with endpoints (2, 3) and (4, 5).
M = ((2 + 4) / 2, (3 + 5) / 2) M = (6 / 2, 8 / 2) M = (3, 4)
Therefore, the midpoint of the line segment is (3, 4).
Understanding Distances
Distance calculations involve finding the length of a line segment or the distance between two points on the coordinate plane. The distance formula is derived from the Pythagorean theorem and is used to calculate the distance between two points (x1, y1) and (x2, y2):
d = √((x2 - x1)^2 + (y2 - y1)^2)
where d is the distance between the two points.
Example: Calculating the Distance
Find the distance between the points (2, 3) and (4, 5).
d = √((4 - 2)^2 + (5 - 3)^2) d = √(2^2 + 2^2) d = √(4 + 4) d = √8 d = 2√2
Therefore, the distance between the two points is 2√2.
6 Ways to Master Midpoint and Distance Calculations
1. Practice with Simple Calculations
Start by practicing midpoint and distance calculations with simple numbers. This will help you become familiar with the formulas and build your confidence in solving problems.
2. Use Graph Paper
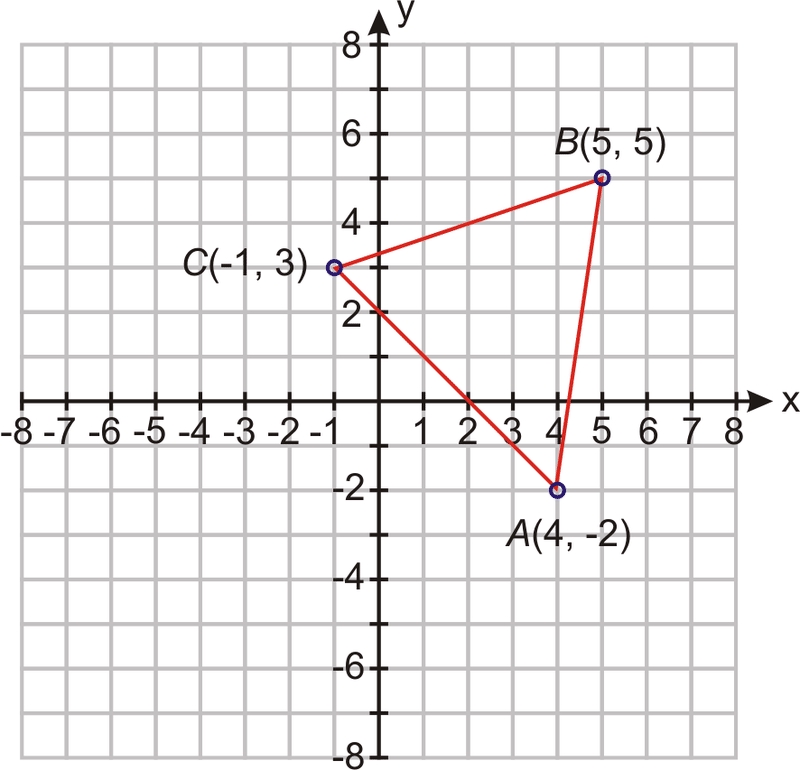
Graph paper can be a valuable tool for visualizing midpoints and distances. By plotting points on the graph paper, you can see the relationships between the points and the line segments.
3. Apply the Formulas to Real-World Problems
Midpoint and distance calculations have numerous real-world applications. Practice applying the formulas to problems involving physics, engineering, architecture, and other fields.
4. Break Down Complex Problems
When dealing with complex problems, break them down into simpler ones. This will help you to identify the midpoints and distances involved and make calculations more manageable.
5. Use Technology
Technology, such as calculators and computer software, can be a powerful tool for midpoint and distance calculations. However, it is essential to understand the underlying formulas and concepts to use technology effectively.
6. Learn from Mistakes
Making mistakes is an inevitable part of the learning process. Analyze your mistakes, identify the errors, and learn from them. This will help you to improve your understanding of midpoint and distance calculations.
🔍 Note: It is essential to double-check your calculations and ensure that you are using the correct formulas and units.
Midpoint and Distance Calculation Table
| Midpoint/Distances | Formula |
|---|---|
| Midpoint | M = ((x1 + x2) / 2, (y1 + y2) / 2) |
| Distance | d = √((x2 - x1)^2 + (y2 - y1)^2) |
Conclusion
Mastering midpoint and distance calculations is a fundamental skill in mathematics and has numerous real-world applications. By following these six ways to master midpoint and distance calculations, you will become proficient in solving problems involving points, lines, and shapes on the coordinate plane.
What is the formula for calculating the midpoint of a line segment?
+The formula for calculating the midpoint of a line segment with endpoints (x1, y1) and (x2, y2) is M = ((x1 + x2) / 2, (y1 + y2) / 2).
What is the formula for calculating the distance between two points?
+The formula for calculating the distance between two points (x1, y1) and (x2, y2) is d = √((x2 - x1)^2 + (y2 - y1)^2).
How can I apply midpoint and distance calculations to real-world problems?
+Midpoint and distance calculations have numerous real-world applications in fields such as physics, engineering, architecture, and more. Practice applying the formulas to problems involving these fields.
Related Terms:
- Midpoint and distance Worksheet pdf
- Midpoint Formula Worksheet pdf
- Midpoint worksheet