Geometry Worksheets Transformations

Geometry Worksheets: Transformations
Transformations are a fundamental concept in geometry, and understanding them is crucial for students to excel in mathematics and other fields like science, engineering, and architecture. In this article, we will explore the different types of transformations, provide examples, and offer geometry worksheets for practice.
What are Transformations in Geometry?
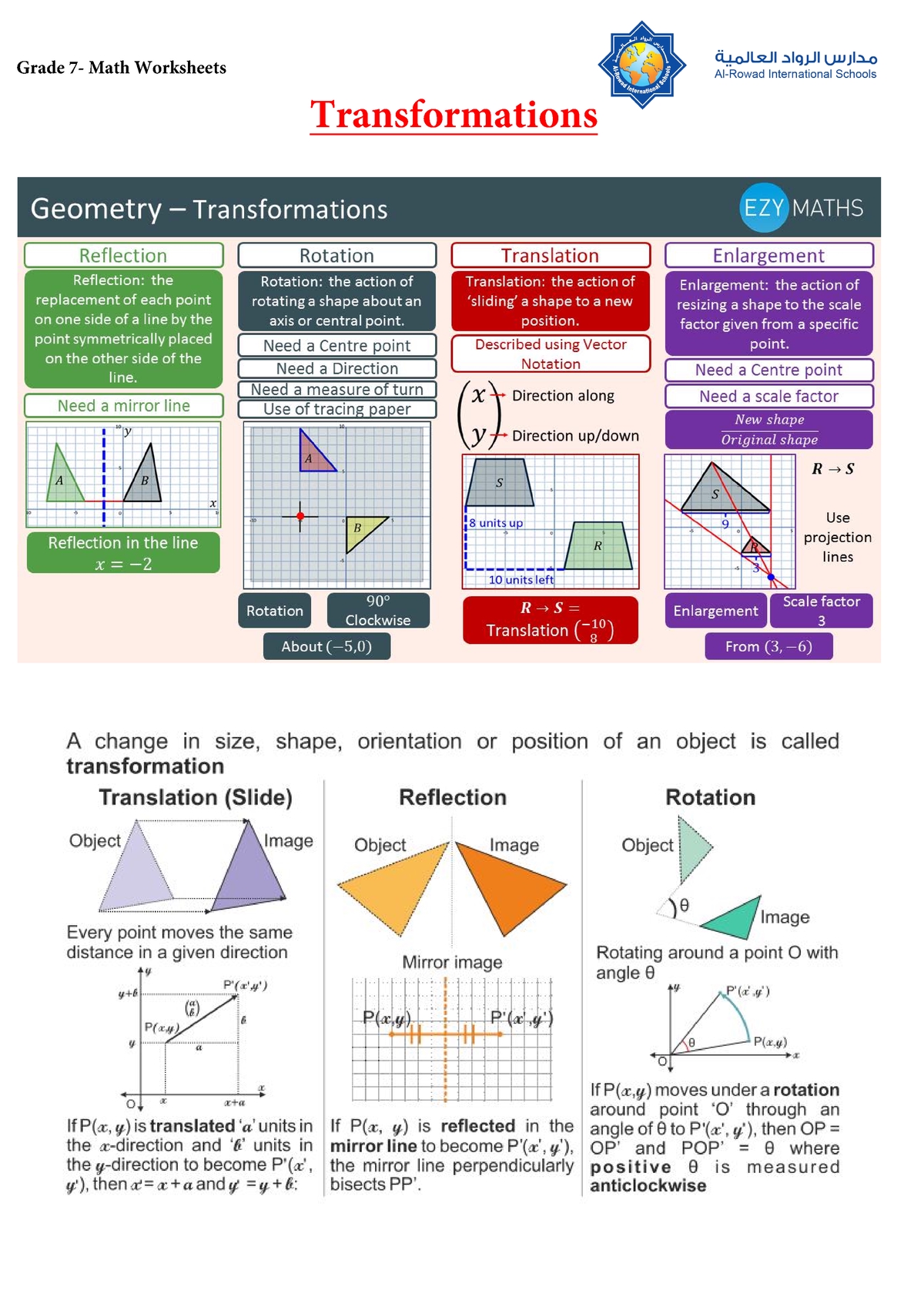
In geometry, a transformation is a way of changing the position or size of a shape. There are four main types of transformations: translation, rotation, reflection, and dilation.
- Translation: Moving a shape from one position to another without changing its size or orientation.
- Rotation: Turning a shape around a fixed point, called the rotation center.
- Reflection: Flipping a shape over a line, called the line of reflection.
- Dilation: Changing the size of a shape, making it larger or smaller.
Types of Transformations
Translation
A translation is a transformation that moves a shape from one position to another without changing its size or orientation. For example, if we have a triangle and we move it 3 units to the right and 2 units up, the resulting triangle is a translation of the original triangle.
Example:
Original Triangle:
A (0, 0) B (2, 0) C (1, 2)
Translated Triangle:
A’ (3, 2) B’ (5, 2) C’ (4, 4)
Rotation
A rotation is a transformation that turns a shape around a fixed point, called the rotation center. For example, if we have a triangle and we rotate it 90 degrees clockwise around the origin, the resulting triangle is a rotation of the original triangle.
Example:
Original Triangle:
A (0, 0) B (2, 0) C (1, 2)
Rotated Triangle:
A’ (0, 0) B’ (0, 2) C’ (-2, 1)
Reflection
A reflection is a transformation that flips a shape over a line, called the line of reflection. For example, if we have a triangle and we reflect it over the x-axis, the resulting triangle is a reflection of the original triangle.
Example:
Original Triangle:
A (0, 0) B (2, 0) C (1, 2)
Reflected Triangle:
A’ (0, 0) B’ (2, 0) C’ (1, -2)
Dilation
A dilation is a transformation that changes the size of a shape, making it larger or smaller. For example, if we have a triangle and we dilate it by a scale factor of 2, the resulting triangle is a dilation of the original triangle.
Example:
Original Triangle:
A (0, 0) B (2, 0) C (1, 2)
Dilated Triangle:
A’ (0, 0) B’ (4, 0) C’ (2, 4)
Geometry Worksheets for Transformations
Here are some geometry worksheets for practicing transformations:
Worksheet 1: Translation
Translate the following shapes 3 units to the right and 2 units up:
| Shape | Original Coordinates | Translated Coordinates |
|---|---|---|
| Triangle | A (0, 0), B (2, 0), C (1, 2) | A’ (3, 2), B’ (5, 2), C’ (4, 4) |
| Square | A (0, 0), B (2, 0), C (2, 2), D (0, 2) | A’ (3, 2), B’ (5, 2), C’ (5, 4), D’ (3, 4) |
Worksheet 2: Rotation
Rotate the following shapes 90 degrees clockwise around the origin:
| Shape | Original Coordinates | Rotated Coordinates |
|---|---|---|
| Triangle | A (0, 0), B (2, 0), C (1, 2) | A’ (0, 0), B’ (0, 2), C’ (-2, 1) |
| Rectangle | A (0, 0), B (2, 0), C (2, 2), D (0, 2) | A’ (0, 0), B’ (0, 2), C’ (-2, 2), D’ (-2, 0) |
Worksheet 3: Reflection
Reflect the following shapes over the x-axis:
| Shape | Original Coordinates | Reflected Coordinates |
|---|---|---|
| Triangle | A (0, 0), B (2, 0), C (1, 2) | A’ (0, 0), B’ (2, 0), C’ (1, -2) |
| Pentagon | A (0, 0), B (2, 0), C (2, 2), D (1, 2), E (0, 2) | A’ (0, 0), B’ (2, 0), C’ (2, -2), D’ (1, -2), E’ (0, -2) |
Worksheet 4: Dilation
Dilate the following shapes by a scale factor of 2:
| Shape | Original Coordinates | Dilated Coordinates |
|---|---|---|
| Triangle | A (0, 0), B (2, 0), C (1, 2) | A’ (0, 0), B’ (4, 0), C’ (2, 4) |
| Circle | Center (0, 0), Radius 2 | Center (0, 0), Radius 4 |
📝 Note: These worksheets are meant to be a starting point for practicing transformations. You can adjust the complexity level and add more exercises as needed.
To reinforce your understanding of transformations, try to create your own geometry worksheets with different shapes and transformation types.
Transformations in Real-Life Applications
Transformations are not just limited to geometry; they have numerous real-life applications in various fields, including:
- Architecture: Transformations are used in building design to create symmetrical and aesthetically pleasing structures.
- Engineering: Transformations are used in the design of mechanical systems, such as gears and levers, to optimize performance and efficiency.
- Computer Graphics: Transformations are used in computer-aided design (CAD) software to create 3D models and animations.
- Art: Transformations are used in various art forms, such as painting and sculpture, to create symmetrical and balanced compositions.
In conclusion, transformations are a fundamental concept in geometry that have numerous real-life applications. By practicing transformations using geometry worksheets, you can develop a deeper understanding of this concept and improve your problem-solving skills.
What are the four main types of transformations in geometry?
+
The four main types of transformations in geometry are translation, rotation, reflection, and dilation.
What is the difference between a translation and a rotation?
+
A translation moves a shape from one position to another without changing its size or orientation, while a rotation turns a shape around a fixed point without changing its size.
What is the difference between a reflection and a dilation?
+
A reflection flips a shape over a line without changing its size, while a dilation changes the size of a shape, making it larger or smaller.
Related Terms:
- Transformation Worksheet pdf
- Translation Worksheet
- Geometry transformation pdf
- IGCSE transformation worksheet pdf
- Rotation worksheet