5 Ways to Solve Multi Step Equations Easily

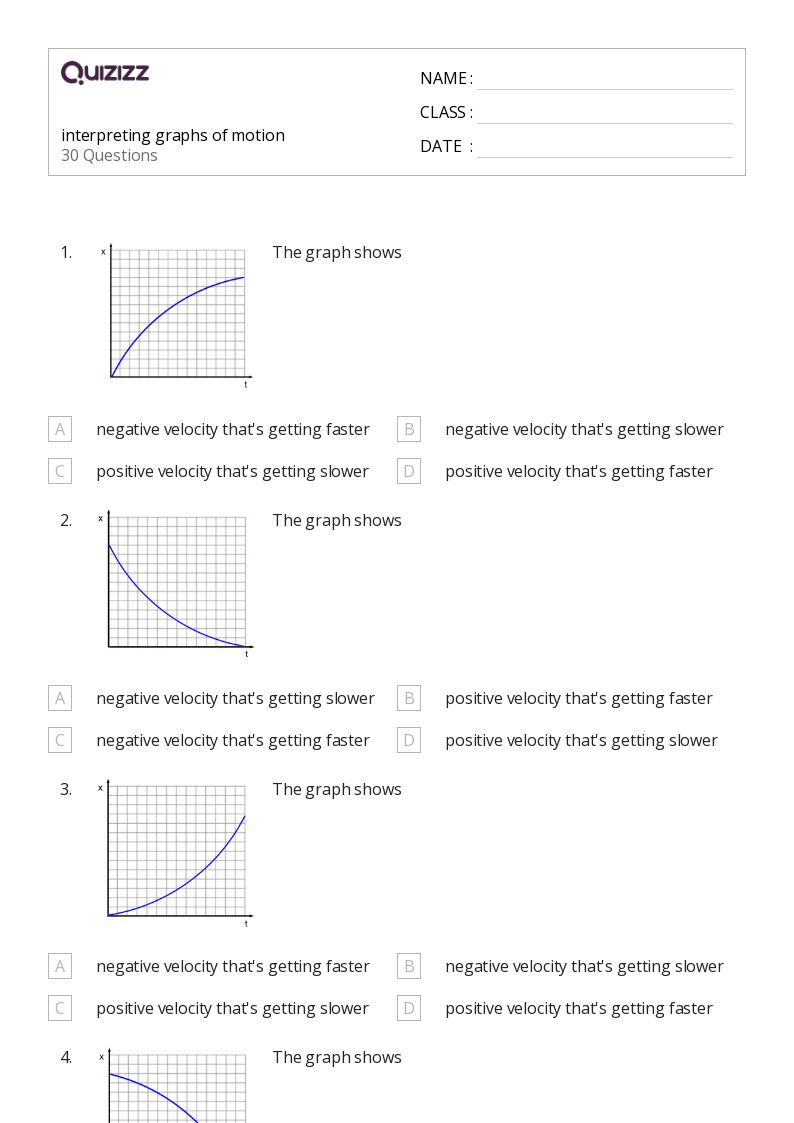
Breaking Down Multi-Step Equations into Manageable Parts
When faced with a multi-step equation, it’s easy to feel overwhelmed. However, with a clear understanding of the steps involved and a few simple strategies, you can solve even the most complex equations with ease. In this article, we’ll explore five ways to solve multi-step equations, breaking down each step into manageable parts.
Understanding the Basics of Multi-Step Equations
Before diving into the strategies, let’s review the basics of multi-step equations. A multi-step equation is an equation that requires more than one step to solve. These equations often involve a combination of addition, subtraction, multiplication, and division operations, as well as variables and constants.
Example: 2x + 5 = 11
To solve this equation, we need to isolate the variable (x) by performing a series of operations. In this case, we need to subtract 5 from both sides and then divide both sides by 2.
Strategy 1: Follow the Order of Operations (PEMDAS)
The first strategy for solving multi-step equations is to follow the order of operations, also known as PEMDAS (Parentheses, Exponents, Multiplication and Division, and Addition and Subtraction). This ensures that you perform the operations in the correct order, avoiding any confusion or errors.
Example: 3(2x - 1) + 2 = 14
Using PEMDAS, we would first evaluate the expression inside the parentheses:
2x - 1 =?
Next, we would multiply the result by 3:
3(2x - 1) = 6x - 3
Finally, we would add 2 to both sides and solve for x:
6x - 3 + 2 = 14 6x - 1 = 14 6x = 15 x = 15⁄6 x = 5⁄2
📝 Note: When using PEMDAS, make sure to evaluate the expressions inside the parentheses first, and then work your way outwards.
Strategy 2: Use Reverse Operations
Another strategy for solving multi-step equations is to use reverse operations. This involves performing the opposite operation to isolate the variable.
Example: x/4 + 2 = 9
To solve this equation, we would first subtract 2 from both sides:
x/4 = 9 - 2 x/4 = 7
Next, we would multiply both sides by 4 to eliminate the fraction:
x = 7 × 4 x = 28
📝 Note: When using reverse operations, make sure to perform the opposite operation to isolate the variable.
Strategy 3: Use the Distributive Property
The distributive property is a powerful tool for solving multi-step equations. This property states that a single operation can be distributed to multiple terms.
Example: 2(x + 3) = 12
Using the distributive property, we would multiply the 2 to both terms inside the parentheses:
2x + 6 = 12
Next, we would subtract 6 from both sides and solve for x:
2x = 12 - 6 2x = 6 x = 6⁄2 x = 3
📝 Note: When using the distributive property, make sure to distribute the operation to all terms inside the parentheses.
Strategy 4: Use Variables to Represent Unknowns
Using variables to represent unknowns is a powerful strategy for solving multi-step equations. This allows you to represent complex relationships between variables and constants.
Example: 2x + 5 = 3x - 2
To solve this equation, we would first add 2 to both sides:
2x + 5 + 2 = 3x - 2 + 2 2x + 7 = 3x
Next, we would subtract 2x from both sides:
7 = 3x - 2x 7 = x
📝 Note: When using variables to represent unknowns, make sure to define the variable clearly and use it consistently throughout the equation.
Strategy 5: Check Your Work
Finally, the fifth strategy for solving multi-step equations is to check your work. This involves plugging your solution back into the original equation to ensure that it is true.
Example: 2x + 5 = 11
We solved this equation earlier, finding that x = 3. To check our work, we would plug x = 3 back into the original equation:
2(3) + 5 = 11 6 + 5 = 11 11 = 11
Since the equation is true, we can be confident that our solution is correct.
📝 Note: When checking your work, make sure to plug your solution back into the original equation to ensure that it is true.
In conclusion, solving multi-step equations requires a combination of strategies and techniques. By following the order of operations, using reverse operations, applying the distributive property, using variables to represent unknowns, and checking your work, you can solve even the most complex equations with ease. Remember to take your time, work step-by-step, and always check your work to ensure accuracy.
What is the order of operations?
+
The order of operations is a set of rules that dictates the order in which mathematical operations should be performed. The acronym PEMDAS is commonly used to remember the order: Parentheses, Exponents, Multiplication and Division, and Addition and Subtraction.
What is the distributive property?
+
The distributive property is a mathematical property that states that a single operation can be distributed to multiple terms. This property is often used to simplify complex equations and expressions.
Why is it important to check your work?
+
Checking your work is an essential step in solving multi-step equations. It ensures that your solution is accurate and helps you catch any errors or mistakes that may have occurred during the solution process.