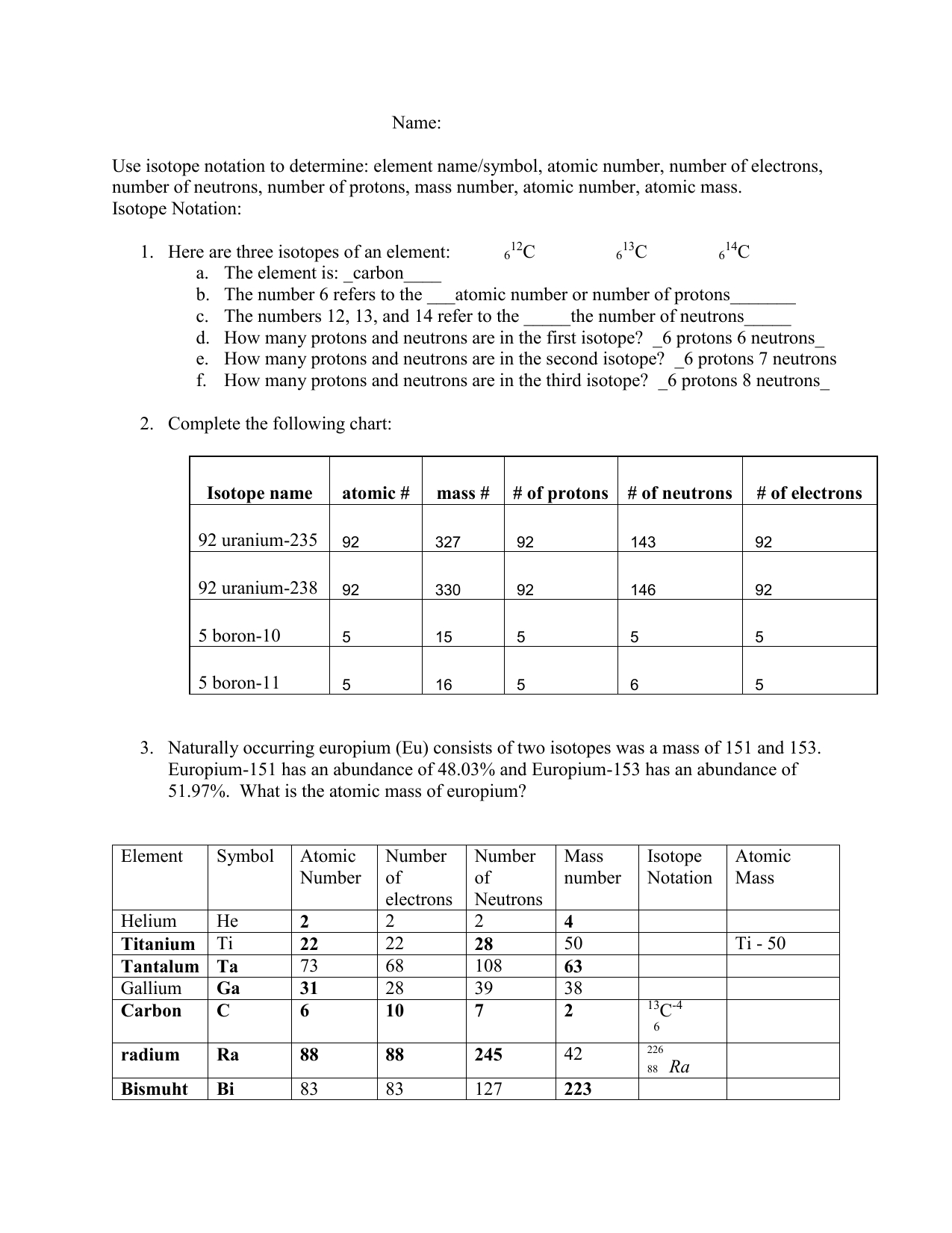
Triangle Congruence SSS and SAS Worksheet Answers

Understanding Triangle Congruence: SSS and SAS

Triangle congruence is a fundamental concept in geometry that helps us determine whether two triangles are identical or not. Two triangles are said to be congruent if their corresponding sides and angles are equal. In this blog post, we will delve into the concept of triangle congruence, focusing on the SSS (Side-Side-Side) and SAS (Side-Angle-Side) postulates.

What is SSS Triangle Congruence?

The SSS postulate states that if three sides of one triangle are equal to the corresponding sides of another triangle, then the two triangles are congruent. This means that if we can show that the three sides of one triangle are equal to the three sides of another triangle, we can conclude that the two triangles are congruent.

SSS Triangle Congruence Theorem:

Theorem: If three sides of one triangle are equal to the corresponding sides of another triangle, then the two triangles are congruent.

Example:

Triangle ABC and Triangle DEF are given. If AB = DE, BC = EF, and AC = DF, then Triangle ABC is congruent to Triangle DEF.

📝 Note: The SSS postulate only requires that the three sides of the triangles be equal, not that the angles be equal.

What is SAS Triangle Congruence?

The SAS postulate states that if two sides and the included angle of one triangle are equal to the corresponding sides and included angle of another triangle, then the two triangles are congruent. This means that if we can show that two sides and the included angle of one triangle are equal to the two sides and included angle of another triangle, we can conclude that the two triangles are congruent.

SAS Triangle Congruence Theorem:

Theorem: If two sides and the included angle of one triangle are equal to the corresponding sides and included angle of another triangle, then the two triangles are congruent.

Example:

Triangle ABC and Triangle DEF are given. If AB = DE, BC = EF, and ∠B = ∠E, then Triangle ABC is congruent to Triangle DEF.

📝 Note: The SAS postulate requires that the included angle be equal, not just any angle.

Key Differences Between SSS and SAS

While both SSS and SAS postulates can be used to determine triangle congruence, there are some key differences between the two:

• SSS requires that all three sides of the triangles be equal, while SAS requires that only two sides and the included angle be equal.
• SSS is often used when we have information about the lengths of the sides of the triangles, while SAS is often used when we have information about the lengths of the sides and the measures of the angles.

Triangle Congruence SSS and SAS Worksheet Answers

Here are some practice problems to help you master the concept of triangle congruence:

SSS Worksheet:

1. Triangle ABC and Triangle DEF are given. If AB = 5, BC = 6, AC = 7, DE = 5, EF = 6, and DF = 7, are the triangles congruent? Answer: Yes, the triangles are congruent by SSS.

2. Triangle GHI and Triangle JKL are given. If GH = 8, HI = 9, GI = 10, JK = 8, KL = 9, and JL = 10, are the triangles congruent? Answer: Yes, the triangles are congruent by SSS.

SAS Worksheet:

1. Triangle ABC and Triangle DEF are given. If AB = 5, BC = 6, ∠B = 60°, DE = 5, EF = 6, and ∠E = 60°, are the triangles congruent? Answer: Yes, the triangles are congruent by SAS.

2. Triangle GHI and Triangle JKL are given. If GH = 8, HI = 9, ∠H = 45°, JK = 8, KL = 9, and ∠K = 45°, are the triangles congruent? Answer: Yes, the triangles are congruent by SAS.

Conclusion

In conclusion, triangle congruence is an important concept in geometry that helps us determine whether two triangles are identical or not. The SSS and SAS postulates provide us with two powerful tools for determining triangle congruence. By mastering these postulates, you will be able to solve a wide range of problems involving triangle congruence.

Related Terms:

• SSS and SAS Congruence Worksheet
• SSS, SAS Worksheet pdf
• SAS Congruence Worksheet pdf
• Triangle Congruence Worksheet answer key
• Triangle Congruence Worksheet PDF