5 Ways to Solve Similar Triangles Easily

Unlocking the Secrets of Similar Triangles
Similar triangles are a fundamental concept in geometry, and understanding how to solve them is crucial for students and professionals alike. Similar triangles have the same shape, but not necessarily the same size. This means that corresponding angles are equal and corresponding sides are in proportion. In this article, we will explore 5 ways to solve similar triangles easily, making it a valuable resource for anyone looking to master this concept.
Method 1: Using the AA Similarity Theorem
The AA Similarity Theorem states that if two angles of one triangle are congruent to two angles of another triangle, then the two triangles are similar. This theorem is useful when you are given two angles of each triangle.
📝 Note: The AA Similarity Theorem is a powerful tool for determining similarity, but it requires that the two angles being compared are corresponding angles.
To use the AA Similarity Theorem, follow these steps:
- Identify the corresponding angles in each triangle.
- Check if the two angles in each triangle are congruent.
- If the angles are congruent, then the triangles are similar.
Method 2: Using the SSS Similarity Theorem
The SSS Similarity Theorem states that if the corresponding sides of two triangles are proportional, then the triangles are similar. This theorem is useful when you are given the lengths of the sides of each triangle.
📝 Note: The SSS Similarity Theorem requires that the corresponding sides are proportional, not necessarily equal.
To use the SSS Similarity Theorem, follow these steps:
- Identify the corresponding sides in each triangle.
- Check if the corresponding sides are proportional.
- If the sides are proportional, then the triangles are similar.
Method 3: Using the SAS Similarity Theorem
The SAS Similarity Theorem states that if two triangles have two sides and the included angle that are proportional, then the triangles are similar. This theorem is useful when you are given two sides and the included angle of each triangle.
📝 Note: The SAS Similarity Theorem requires that the two sides and the included angle are proportional, not necessarily equal.
To use the SAS Similarity Theorem, follow these steps:
- Identify the corresponding sides and included angle in each triangle.
- Check if the corresponding sides and included angle are proportional.
- If the sides and included angle are proportional, then the triangles are similar.
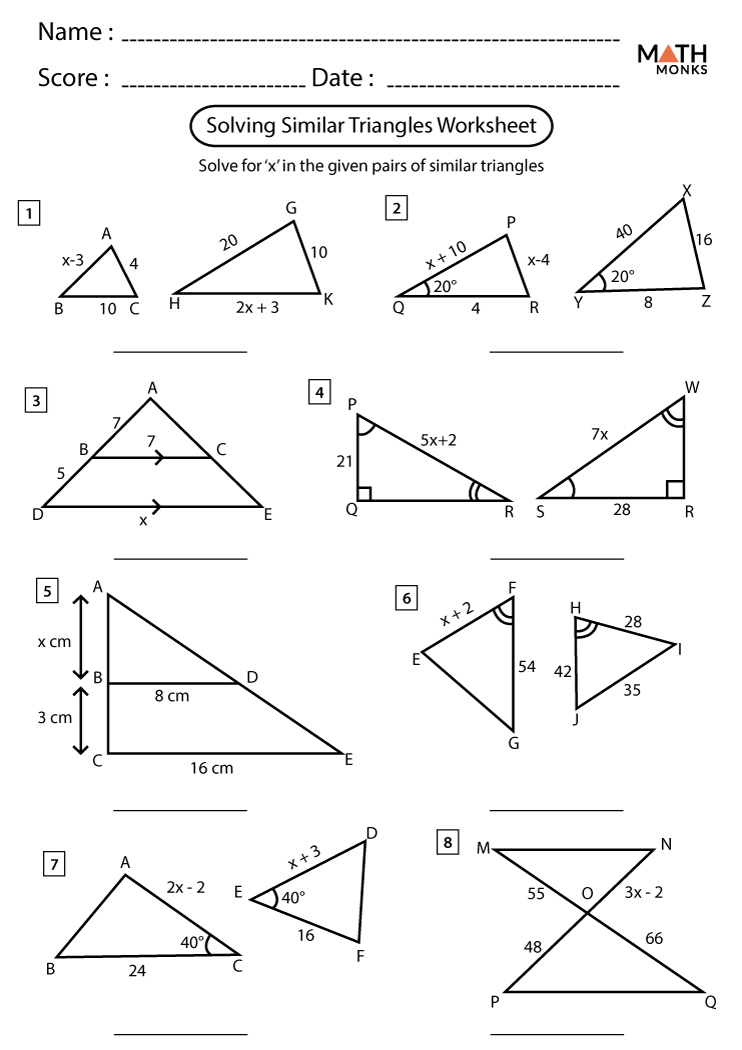
Method 4: Using the Side-Splitting Theorem
The Side-Splitting Theorem states that if a line intersects two sides of a triangle and the ratios of the lengths of the segments are equal, then the line is parallel to the third side.
📝 Note: The Side-Splitting Theorem requires that the line intersects two sides of the triangle.
To use the Side-Splitting Theorem, follow these steps:
- Draw a diagram of the triangle with the intersecting line.
- Identify the corresponding segments in each triangle.
- Check if the ratios of the lengths of the segments are equal.
- If the ratios are equal, then the line is parallel to the third side.
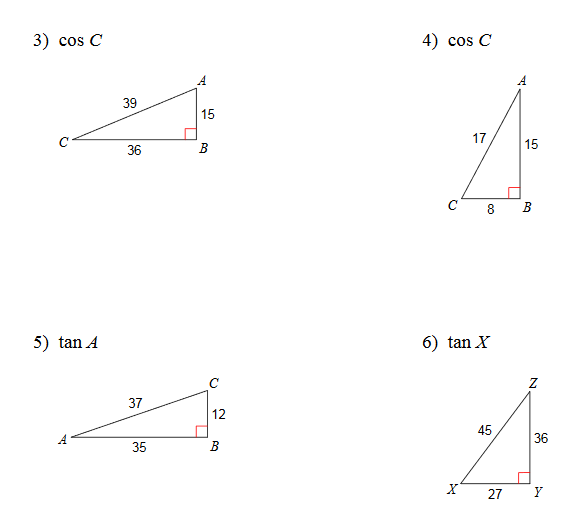
Method 5: Using the Pythagorean Theorem
The Pythagorean Theorem states that in a right triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
📝 Note: The Pythagorean Theorem only applies to right triangles.
To use the Pythagorean Theorem, follow these steps:
- Identify the right triangle and the corresponding sides.
- Plug in the values of the sides into the Pythagorean Theorem formula.
- Solve for the unknown side.
| Method | Description |
|---|---|
| AA Similarity Theorem | Two angles of one triangle are congruent to two angles of another triangle. |
| SSS Similarity Theorem | Corresponding sides of two triangles are proportional. |
| SAS Similarity Theorem | Two sides and the included angle of two triangles are proportional. |
| Side-Splitting Theorem | A line intersects two sides of a triangle and the ratios of the lengths of the segments are equal. |
| Pythagorean Theorem | The square of the hypotenuse of a right triangle is equal to the sum of the squares of the other two sides. |
In conclusion, solving similar triangles is a crucial skill in geometry, and using the right methods can make it easy. By understanding the AA Similarity Theorem, SSS Similarity Theorem, SAS Similarity Theorem, Side-Splitting Theorem, and Pythagorean Theorem, you can master the art of solving similar triangles. Remember to identify the corresponding angles and sides, and to use the correct theorem to determine similarity.
What is the difference between AA Similarity Theorem and SSS Similarity Theorem?
+The AA Similarity Theorem requires that two angles of one triangle are congruent to two angles of another triangle, while the SSS Similarity Theorem requires that the corresponding sides of two triangles are proportional.
Can I use the Pythagorean Theorem to solve any triangle?
+No, the Pythagorean Theorem only applies to right triangles. If the triangle is not a right triangle, you cannot use the Pythagorean Theorem to solve it.
What is the Side-Splitting Theorem used for?
+The Side-Splitting Theorem is used to determine if a line is parallel to the third side of a triangle. It requires that the line intersects two sides of the triangle and the ratios of the lengths of the segments are equal.
Related Terms:
- Similar triangles missing sides Worksheet
- Parts of similar triangles Worksheet
- Similar triangles angles Worksheet
- Similar triangles Proportions Worksheet pdf