Solving and Graphing Inequalities Made Easy for Students
Unlocking the Secrets of Solving and Graphing Inequalities
Are you tired of feeling overwhelmed by inequalities in math? Do you struggle to understand the concepts of solving and graphing inequalities? You’re not alone! Many students find inequalities to be a challenging topic, but with the right approach, it can be made easy.
In this article, we’ll explore the world of inequalities, breaking down the concepts into simple, bite-sized chunks. We’ll cover the basics of solving and graphing inequalities, providing you with the tools and confidence you need to tackle even the toughest problems.
What are Inequalities?
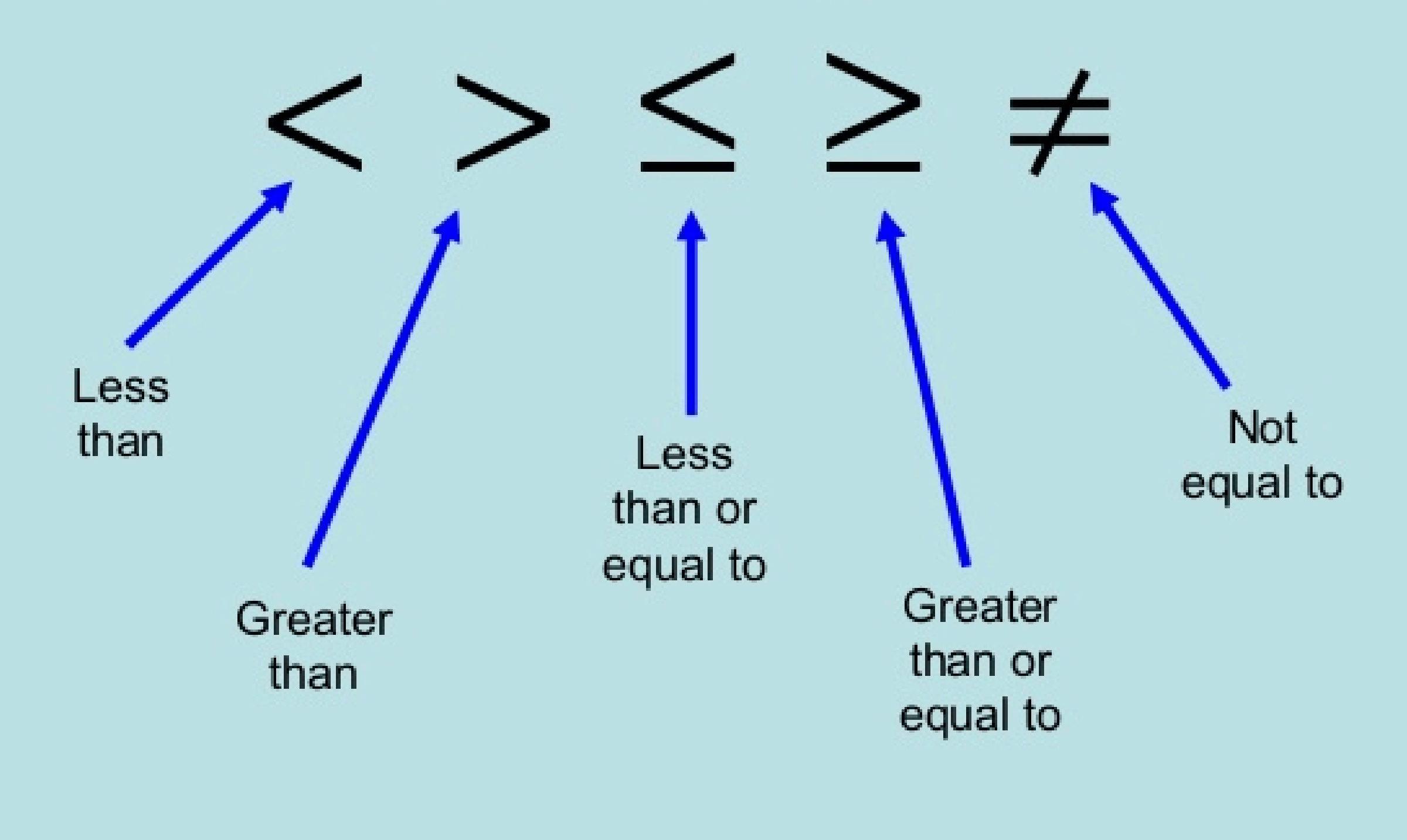
Before we dive into solving and graphing inequalities, let’s first define what an inequality is. An inequality is a statement that compares two expressions using one of the following symbols:
- Less than (<)
- Greater than (>)
- Less than or equal to (≤)
- Greater than or equal to (≥)
For example, 2x + 3 > 5 is an inequality that compares the expression 2x + 3 to the value 5.
Solving Inequalities
Solving an inequality involves finding the values of the variable that make the inequality true. There are several steps to follow when solving an inequality:
- Add or subtract the same value to both sides: This will help you isolate the variable.
- Multiply or divide both sides by the same value: This will help you get rid of any coefficients.
- Flip the inequality sign when dividing by a negative number: This is a crucial step to remember!
Let’s solve a simple inequality to illustrate these steps:
Solve for x: 2x + 3 > 5
- Subtract 3 from both sides: 2x > 2
- Divide both sides by 2: x > 1
📝 Note: When solving inequalities, it's essential to keep track of the direction of the inequality sign.
Graphing Inequalities
Graphing inequalities involves visualizing the solution on a number line or coordinate plane. There are two types of inequality graphs:
- Open circles: Used to represent strict inequalities (less than or greater than)
- Closed circles: Used to represent non-strict inequalities (less than or equal to or greater than or equal to)
Let’s graph the inequality we solved earlier:
x > 1
This inequality represents an open circle at x = 1, with the arrow pointing to the right.

| x | y |
|---|---|
| 1 | • |
| 2 | ⊃ |
Special Cases: Absolute Value Inequalities
Absolute value inequalities can be a bit trickier to solve. The key is to consider the distance between the variable and the value.
For example, solve for x: |x - 2| > 3
This inequality represents the distance between x and 2 being greater than 3.
To solve this inequality, we’ll split it into two separate inequalities:
x - 2 > 3 or x - 2 < -3
Simplifying these inequalities, we get:
x > 5 or x < -1
📝 Note: When solving absolute value inequalities, always consider the distance between the variable and the value.
Conclusion
Solving and graphing inequalities may seem daunting at first, but with practice and patience, you’ll become a pro in no time. Remember to follow the steps, keep track of the inequality sign, and visualize the solution on a number line or coordinate plane.
Inequalities are an essential part of math, and mastering them will open doors to more advanced topics. So, don’t be afraid to tackle inequalities head-on – with this guide, you’ll be solving and graphing like a pro in no time!
What is the difference between a strict inequality and a non-strict inequality?
+A strict inequality uses the symbols < or >, while a non-strict inequality uses the symbols ≤ or ≥.
How do I graph an inequality on a number line?
+To graph an inequality on a number line, draw an open or closed circle at the boundary value, and then draw an arrow pointing to the left or right to represent the solution.
What is the purpose of flipping the inequality sign when dividing by a negative number?
+Flipping the inequality sign when dividing by a negative number ensures that the solution is accurate, as the direction of the inequality changes when dividing by a negative value.