Exponent Rules and Properties Worksheet for Students
Understanding Exponent Rules and Properties
Exponents are a fundamental concept in mathematics, and mastering their rules and properties is essential for solving various mathematical problems. In this article, we will delve into the world of exponents, exploring their definition, rules, and properties, along with examples and exercises to help students solidify their understanding.
What are Exponents?
Exponents are shorthand notation for repeated multiplication. They consist of a base number and an exponent, which represents the number of times the base is multiplied by itself. For instance, the expression 2^3 represents 2 multiplied by itself three times: 2 × 2 × 2 = 8.
Rules of Exponents
There are several rules of exponents that help simplify expressions and equations. Here are some of the most important ones:
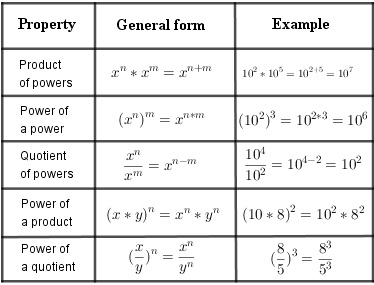
1. Product of Powers Rule
When multiplying two powers with the same base, add the exponents.
Example: 2^2 × 2^3 = 2^(2+3) = 2^5
2. Power of a Power Rule
When raising a power to another power, multiply the exponents.
Example: (2^2)^3 = 2^(2×3) = 2^6
3. Power of a Product Rule
When raising a product to a power, raise each factor to that power.
Example: (2 × 3)^2 = 2^2 × 3^2 = 4 × 9 = 36
4. Zero Exponent Rule
Any non-zero number raised to the power of zero is equal to 1.
Example: 2^0 = 1
5. Negative Exponent Rule
A negative exponent is equivalent to the reciprocal of the base raised to the positive exponent.
Example: 2^(-3) = 1 / 2^3 = 1⁄8
Properties of Exponents
Exponents have several important properties that make them useful in mathematical expressions.
1. Commutative Property
The order of the bases does not change the result.
Example: 2^3 × 3^2 = 3^2 × 2^3
2. Associative Property
The order in which we multiply powers with the same base does not change the result.
Example: (2^2 × 2^3) × 2^4 = 2^2 × (2^3 × 2^4)
3. Distributive Property
Exponents can be distributed over addition and subtraction.
Example: 2^(3+2) = 2^3 × 2^2
Worksheet Exercises
Now that you have learned the rules and properties of exponents, it’s time to practice! Here are some exercises to help you reinforce your understanding:
Exercise 1: Simplify the following expressions:
- 2^2 × 2^4 =
- (3^2)^3 =
- 2^(-2) =
Exercise 2: Solve the following equations:
- 2^x = 16
- 3^(2x) = 81
Exercise 3: Evaluate the following expressions:
- 2^3 + 2^2 =
- 3^2 × 3^(-2) =
📝 Note: Remember to apply the rules and properties of exponents to simplify expressions and solve equations.
Conclusion
In this article, we have explored the world of exponents, covering their definition, rules, and properties. We have also provided exercises to help you practice and reinforce your understanding. By mastering the rules and properties of exponents, you will be able to simplify complex expressions and solve equations with ease.
What is the product of powers rule?
+
The product of powers rule states that when multiplying two powers with the same base, you add the exponents.
What is the power of a power rule?
+
The power of a power rule states that when raising a power to another power, you multiply the exponents.
What is the zero exponent rule?
+
The zero exponent rule states that any non-zero number raised to the power of zero is equal to 1.



