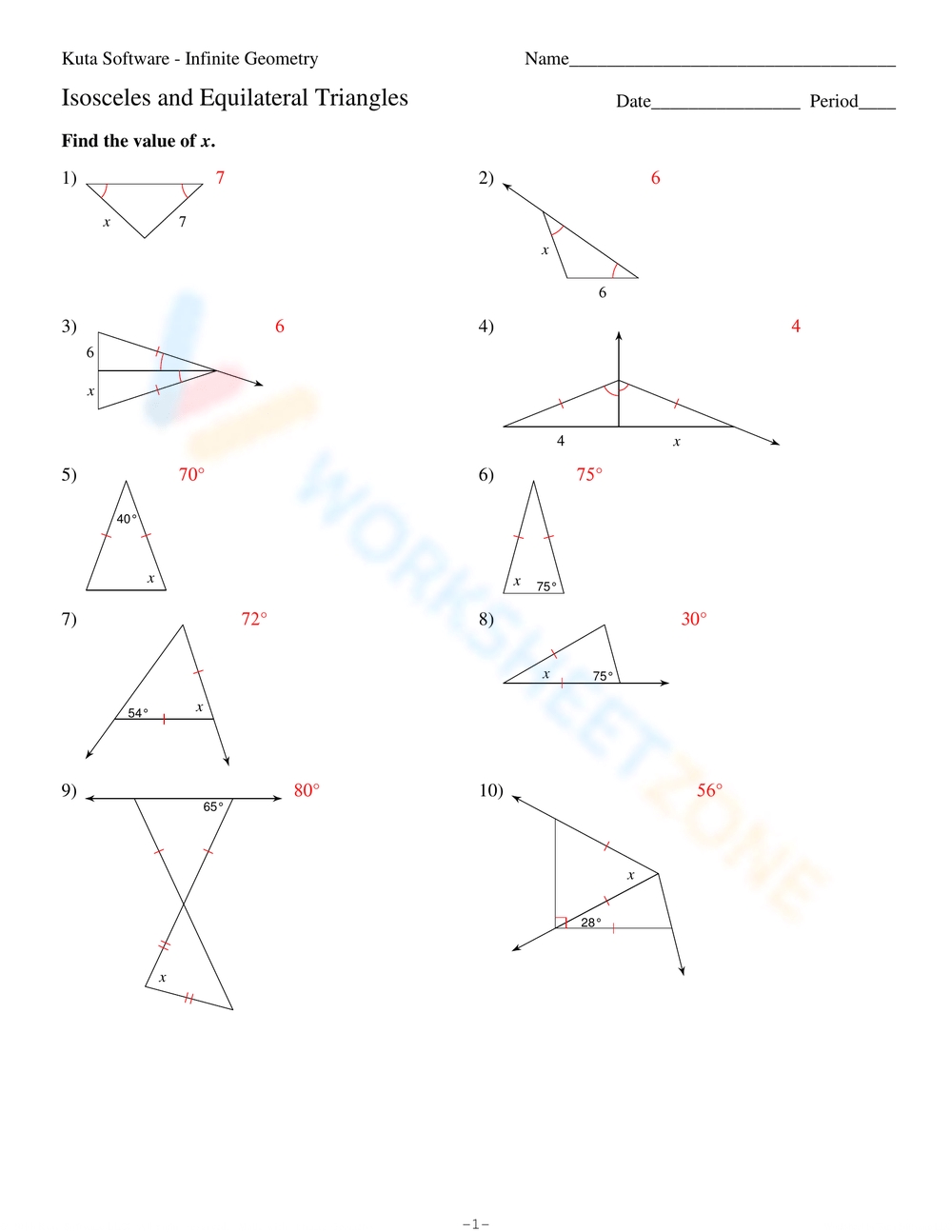
Isosceles and Equilateral Triangles Worksheet Solutions
Understanding Isosceles and Equilateral Triangles
Triangles are one of the most basic shapes in geometry, and they can be classified into different types based on their properties. Two common types of triangles are isosceles and equilateral triangles. In this blog post, we will explore the properties and characteristics of these two types of triangles, and provide solutions to common problems.
Isosceles Triangles
An isosceles triangle is a triangle that has two sides of equal length. The two equal sides are called the legs of the triangle, and the third side is called the base. The angles opposite the equal sides are also equal, and are called the base angles.
Properties of Isosceles Triangles:
- Two sides of equal length
- Two equal angles (base angles)
- The base angles are opposite the equal sides
- The third side (base) is not necessarily equal to the other two sides
Equilateral Triangles
An equilateral triangle is a triangle that has all three sides of equal length. Since all three sides are equal, all three angles are also equal. Each angle in an equilateral triangle is 60 degrees.
Properties of Equilateral Triangles:
- All three sides of equal length
- All three angles of equal measure (60 degrees)
- All sides and angles are congruent
Solutions to Common Problems
Here are some common problems related to isosceles and equilateral triangles, along with their solutions:
Problem 1:
In an isosceles triangle, the base angles are 30 degrees each. What is the measure of the third angle?
Solution:
Since the base angles are 30 degrees each, we know that the third angle is equal to 180 - 30 - 30 = 120 degrees.
Problem 2:
In an equilateral triangle, one side is 6 cm long. What is the perimeter of the triangle?
Solution:
Since all three sides of an equilateral triangle are equal, the perimeter is equal to 3 x 6 = 18 cm.
Problem 3:
In an isosceles triangle, the legs are 8 cm long, and the base is 10 cm long. What is the height of the triangle?
Solution:
We can use the Pythagorean theorem to find the height of the triangle:
height^2 + (base/2)^2 = leg^2
Plugging in the values, we get:
height^2 + (10⁄2)^2 = 8^2 height^2 + 5^2 = 64 height^2 = 39 height = √39
Table: Comparison of Isosceles and Equilateral Triangles
| Isosceles Triangle | Equilateral Triangle | |
|---|---|---|
| Number of equal sides | 2 | 3 |
| Number of equal angles | 2 | 3 |
| Measure of equal angles | variable | 60 degrees |
| Perimeter | variable | 3 x side length |
📝 Note: This table is a summary of the properties of isosceles and equilateral triangles. It is not an exhaustive list of all properties, but rather a comparison of the two types of triangles.
Conclusion
In this blog post, we have explored the properties and characteristics of isosceles and equilateral triangles. We have also provided solutions to common problems related to these two types of triangles. By understanding the properties of these triangles, we can better solve problems and apply geometric concepts to real-world situations.
What is the main difference between an isosceles triangle and an equilateral triangle?
+The main difference between an isosceles triangle and an equilateral triangle is the number of equal sides. An isosceles triangle has two equal sides, while an equilateral triangle has three equal sides.
What is the measure of each angle in an equilateral triangle?
+Each angle in an equilateral triangle is 60 degrees.
What is the perimeter of an equilateral triangle with side length 5 cm?
+The perimeter of an equilateral triangle with side length 5 cm is 3 x 5 = 15 cm.
Related Terms:
- Isosceles and equilateral triangles theorems
- Isosceles triangle Worksheet answer Key
- Isosceles and equilateral triangles Notes
- Isosceles and equilateral triangles practice