5 Ways to Transform Quadratic Functions
Quadratic functions are a fundamental concept in algebra, and transforming them can be a powerful tool for solving equations and graphing curves. In this article, we will explore five ways to transform quadratic functions, including shifting, stretching, compressing, reflecting, and rotating.
Understanding Quadratic Functions
A quadratic function is a polynomial function of degree two, which means the highest power of the variable is two. The general form of a quadratic function is:
f(x) = ax^2 + bx + c
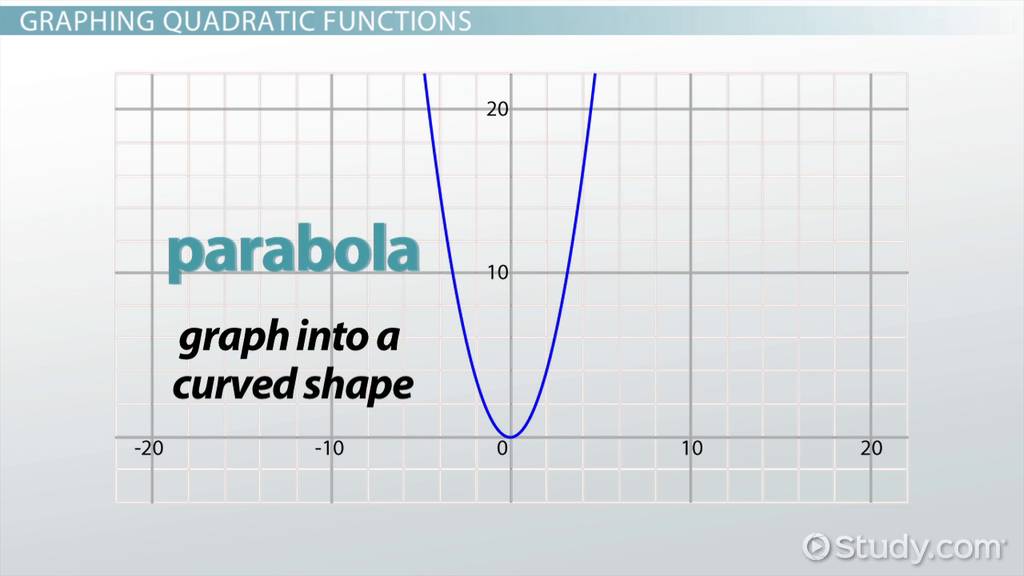
where a, b, and c are constants. The graph of a quadratic function is a parabola, which is a U-shaped curve that opens upwards or downwards.
1. Shifting Quadratic Functions
Shifting a quadratic function involves moving the graph of the function horizontally or vertically. There are two types of shifts: horizontal shifts and vertical shifts.
- Horizontal Shifts: A horizontal shift involves moving the graph of the function to the left or right by a certain number of units. To shift a quadratic function horizontally, add or subtract a constant from the x-term.
f(x) = a(x - h)^2 + k
where h is the horizontal shift. * Vertical Shifts: A vertical shift involves moving the graph of the function up or down by a certain number of units. To shift a quadratic function vertically, add or subtract a constant from the y-term.
f(x) = a(x)^2 + k
where k is the vertical shift.
💡 Note: When shifting a quadratic function, the vertex of the parabola moves accordingly.
2. Stretching and Compressing Quadratic Functions
Stretching and compressing a quadratic function involves changing the width of the parabola. There are two types of stretches and compressions: vertical stretches and compressions, and horizontal stretches and compressions.
- Vertical Stretches and Compressions: A vertical stretch or compression involves changing the height of the parabola. To stretch or compress a quadratic function vertically, multiply the entire function by a constant.
f(x) = a(cx)^2
where c is the vertical stretch or compression factor. * Horizontal Stretches and Compressions: A horizontal stretch or compression involves changing the width of the parabola. To stretch or compress a quadratic function horizontally, divide the x-term by a constant.
f(x) = a(x/c)^2
where c is the horizontal stretch or compression factor.
📝 Note: When stretching or compressing a quadratic function, the vertex of the parabola remains unchanged.
3. Reflecting Quadratic Functions
Reflecting a quadratic function involves flipping the graph of the function over a horizontal or vertical axis.
- Reflection over the x-axis: To reflect a quadratic function over the x-axis, multiply the entire function by -1.
f(x) = -a(x)^2 + c
- Reflection over the y-axis: To reflect a quadratic function over the y-axis, replace x with -x.
f(x) = a(-x)^2 + c
🔮 Note: When reflecting a quadratic function, the vertex of the parabola changes accordingly.
4. Rotating Quadratic Functions
Rotating a quadratic function involves rotating the graph of the function by a certain angle.
- Rotation by 90 degrees: To rotate a quadratic function by 90 degrees, replace x with y and y with -x.
f(x) = a(y)^2 + c f(y) = -a(x)^2 + c
- Rotation by 180 degrees: To rotate a quadratic function by 180 degrees, replace x with -x and y with -y.
f(x) = a(-x)^2 + c f(y) = a(-y)^2 + c
🔄 Note: When rotating a quadratic function, the vertex of the parabola changes accordingly.
5. Combining Transformations
In many cases, we may need to combine multiple transformations to achieve the desired result. For example, we may need to shift and stretch a quadratic function simultaneously.
f(x) = a(cx - h)^2 + k
In this case, we first shift the function horizontally by h units, then stretch or compress it vertically by a factor of c, and finally shift it vertically by k units.
In conclusion, transforming quadratic functions is a powerful tool for solving equations and graphing curves. By understanding how to shift, stretch, compress, reflect, and rotate quadratic functions, we can manipulate the graph of a quadratic function to achieve the desired result.
What is a quadratic function?
+A quadratic function is a polynomial function of degree two, which means the highest power of the variable is two.
How do I shift a quadratic function horizontally?
+To shift a quadratic function horizontally, add or subtract a constant from the x-term.
How do I stretch a quadratic function vertically?
+To stretch a quadratic function vertically, multiply the entire function by a constant.
Related Terms:
- Vertex form Transformations Worksheet
- Quadratic transformations rules