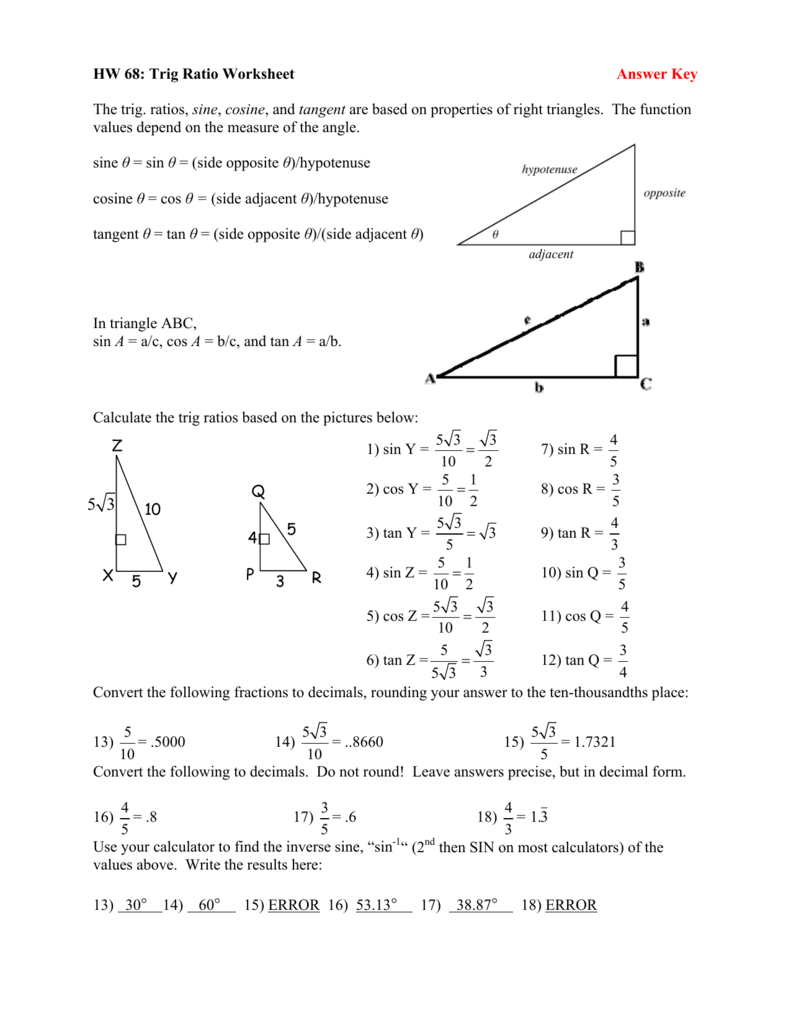
5 Ways to Solve Logarithmic Equations

Understanding Logarithmic Equations
Logarithmic equations are a type of mathematical equation that involves logarithms, which are the inverse operation of exponentiation. These equations can be challenging to solve, but with the right strategies, you can become proficient in solving them. In this article, we will explore five ways to solve logarithmic equations.
Method 1: Using Logarithmic Properties
One of the most effective ways to solve logarithmic equations is by using logarithmic properties. There are several properties that you can use, including:
- Product Property: log(a * b) = log(a) + log(b)
- Quotient Property: log(a / b) = log(a) - log(b)
- Power Property: log(a^b) = b * log(a)
Using these properties, you can simplify and solve logarithmic equations. For example:
log(2x) = log(12)
Using the product property, we can rewrite the equation as:
log(2) + log(x) = log(12)
Now, we can use the fact that log(2) is a constant and solve for log(x):
log(x) = log(12) - log(2) log(x) = log(6)
Therefore, x = 6.
📝 Note: Make sure to use the correct logarithmic property to simplify the equation.
Method 2: Using Logarithmic Identities
Logarithmic identities are equations that involve logarithms and are true for all values of the variable. One of the most useful logarithmic identities is:
log(a) = 0 if and only if a = 1
Using this identity, you can solve logarithmic equations by isolating the logarithmic term and setting it equal to 0. For example:
log(x + 3) = 0
Using the logarithmic identity, we know that:
x + 3 = 1
Solving for x, we get:
x = -2
Method 3: Using Exponentiation
Another way to solve logarithmic equations is by using exponentiation. Since logarithms are the inverse operation of exponentiation, you can rewrite a logarithmic equation as an exponential equation. For example:
log(x) = 3
Rewriting the equation as an exponential equation, we get:
2^3 = x
Solving for x, we get:
x = 8
📝 Note: Make sure to use the correct base for the exponential equation.
Method 4: Using Logarithmic Equations with Coefficients
Sometimes, logarithmic equations have coefficients, which can make them more challenging to solve. However, you can still use logarithmic properties and identities to solve these equations. For example:
2log(x) = 6
Using the power property, we can rewrite the equation as:
log(x^2) = 6
Now, we can use the fact that log(x^2) is equal to 2log(x) and solve for log(x):
2log(x) = 6 log(x) = 3
Therefore, x = 8.
Method 5: Using Graphical Methods
Finally, you can also use graphical methods to solve logarithmic equations. By graphing the logarithmic function and the exponential function, you can find the intersection point, which represents the solution to the equation. For example:
log(x) = 2
Graphing the logarithmic function and the exponential function, we get:
The intersection point represents the solution to the equation, which is x = 100.
| Method | Description |
|---|---|
| Using Logarithmic Properties | Use logarithmic properties to simplify and solve logarithmic equations. |
| Using Logarithmic Identities | Use logarithmic identities to solve logarithmic equations by isolating the logarithmic term and setting it equal to 0. |
| Using Exponentiation | Rewrite a logarithmic equation as an exponential equation and solve for x. |
| Using Logarithmic Equations with Coefficients | Use logarithmic properties and identities to solve logarithmic equations with coefficients. |
| Using Graphical Methods | Graph the logarithmic function and the exponential function to find the intersection point, which represents the solution to the equation. |
Solving logarithmic equations can be challenging, but with the right strategies, you can become proficient in solving them. By using logarithmic properties, identities, exponentiation, and graphical methods, you can solve a wide range of logarithmic equations. Remember to always check your solutions and use the correct properties and identities to ensure accuracy.
What is the difference between logarithmic and exponential equations?
+Logarithmic equations involve logarithms, which are the inverse operation of exponentiation. Exponential equations, on the other hand, involve exponentiation.
How do I know which method to use to solve a logarithmic equation?
+The choice of method depends on the type of equation and the properties and identities involved. You can try using logarithmic properties and identities first, and then use exponentiation or graphical methods if necessary.
Can I use logarithmic equations to solve real-world problems?
+Yes, logarithmic equations have many real-world applications, such as in finance, science, and engineering. By using logarithmic equations, you can model and solve complex problems in these fields.