5 Ways to Master Quadratic Graphs

Unlocking the Secrets of Quadratic Graphs: A Comprehensive Guide
Quadratic graphs are a fundamental concept in mathematics, and mastering them is essential for success in various fields, including physics, engineering, and computer science. In this article, we will explore five ways to help you master quadratic graphs and become proficient in analyzing and interpreting these complex curves.
Understanding the Basics
Before diving into the advanced techniques, it’s crucial to understand the basics of quadratic graphs. A quadratic graph is a type of polynomial function that can be written in the form of ax^2 + bx + c, where a, b, and c are constants. The graph of a quadratic function is a parabola, which can be either concave up or concave down.
📝 Note: To understand quadratic graphs, you need to be familiar with the concept of functions, variables, and graphing.
Method 1: Factoring Quadratic Expressions
Factoring quadratic expressions is a powerful technique for analyzing and solving quadratic equations. By factoring a quadratic expression, you can identify the roots of the equation, which are the points where the graph intersects the x-axis.
For example, consider the quadratic expression x^2 + 5x + 6. By factoring, we get (x + 3)(x + 2) = 0, which gives us the roots x = -3 and x = -2.
| Quadratic Expression | Factored Form | Roots |
|---|---|---|
| x^2 + 5x + 6 | (x + 3)(x + 2) | x = -3, x = -2 |
Method 2: Using the Quadratic Formula
The quadratic formula is a powerful tool for solving quadratic equations. The formula is given by:
x = (-b ± √(b^2 - 4ac)) / 2a
where a, b, and c are the coefficients of the quadratic equation.
For example, consider the quadratic equation x^2 + 4x + 4 = 0. Using the quadratic formula, we get:
x = (-4 ± √(4^2 - 4(1)(4))) / 2(1) x = (-4 ± √(16 - 16)) / 2 x = (-4 ± √0) / 2 x = -2
📝 Note: The quadratic formula can be used to solve quadratic equations that cannot be factored easily.
Method 3: Graphing Quadratic Functions
Graphing quadratic functions is an essential skill for visualizing and analyzing the behavior of quadratic graphs. By graphing a quadratic function, you can identify the maximum or minimum point, the axis of symmetry, and the roots of the equation.
For example, consider the quadratic function f(x) = x^2 + 2x + 1. By graphing the function, we can see that the graph is a parabola that opens upward, with a minimum point at (-1, 0).
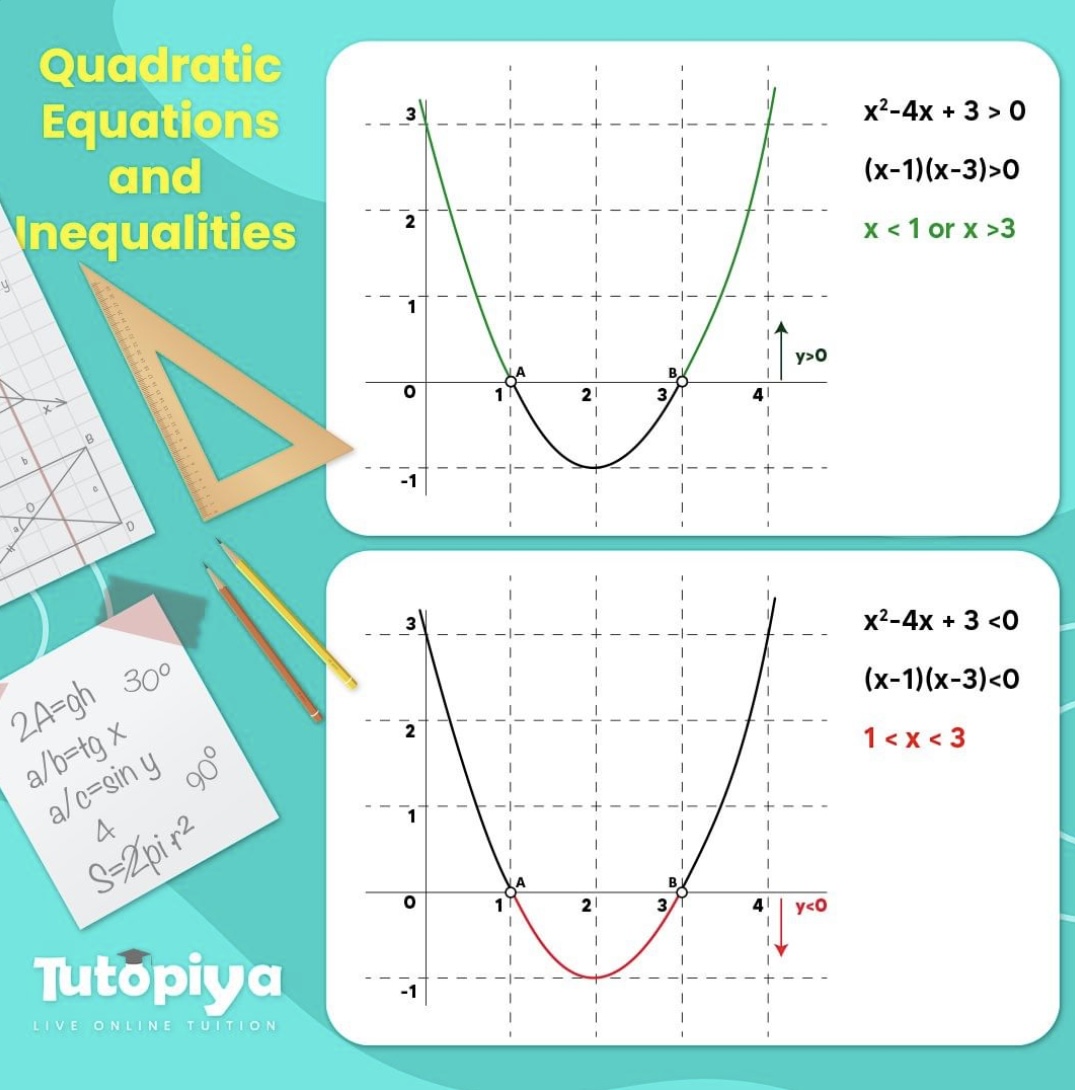
Method 4: Analyzing Quadratic Graphs
Analyzing quadratic graphs involves identifying the key features of the graph, such as the axis of symmetry, the maximum or minimum point, and the roots of the equation.
For example, consider the quadratic graph shown below:
[Insert image of a quadratic graph]
By analyzing the graph, we can see that the axis of symmetry is x = -2, the maximum point is (-2, 4), and the roots of the equation are x = -3 and x = -1.
Method 5: Using Technology to Explore Quadratic Graphs
Technology can be a powerful tool for exploring and analyzing quadratic graphs. By using graphing calculators or computer software, you can visualize and interact with quadratic graphs in a dynamic and engaging way.
For example, consider using a graphing calculator to explore the quadratic function f(x) = x^2 + 2x + 1. By adjusting the coefficients and constants, you can see how the graph changes and how the key features of the graph are affected.
What is the difference between a quadratic equation and a quadratic function?
+A quadratic equation is a polynomial equation of degree two, while a quadratic function is a function that can be written in the form of ax^2 + bx + c.
How do I identify the axis of symmetry of a quadratic graph?
+The axis of symmetry of a quadratic graph is the vertical line that passes through the vertex of the parabola.
What is the quadratic formula, and how is it used?
+The quadratic formula is a powerful tool for solving quadratic equations. It is given by x = (-b ± √(b^2 - 4ac)) / 2a, where a, b, and c are the coefficients of the quadratic equation.
By mastering the five methods outlined in this article, you will become proficient in analyzing and interpreting quadratic graphs. Remember to practice regularly and use technology to enhance your understanding of these complex curves. With time and effort, you will become an expert in quadratic graphs and be able to tackle even the most challenging problems with confidence.