Master 8 2 Trigonometric Ratios with This Simple Worksheet
Mastering Trigonometric Ratios: A Simple yet Effective Guide
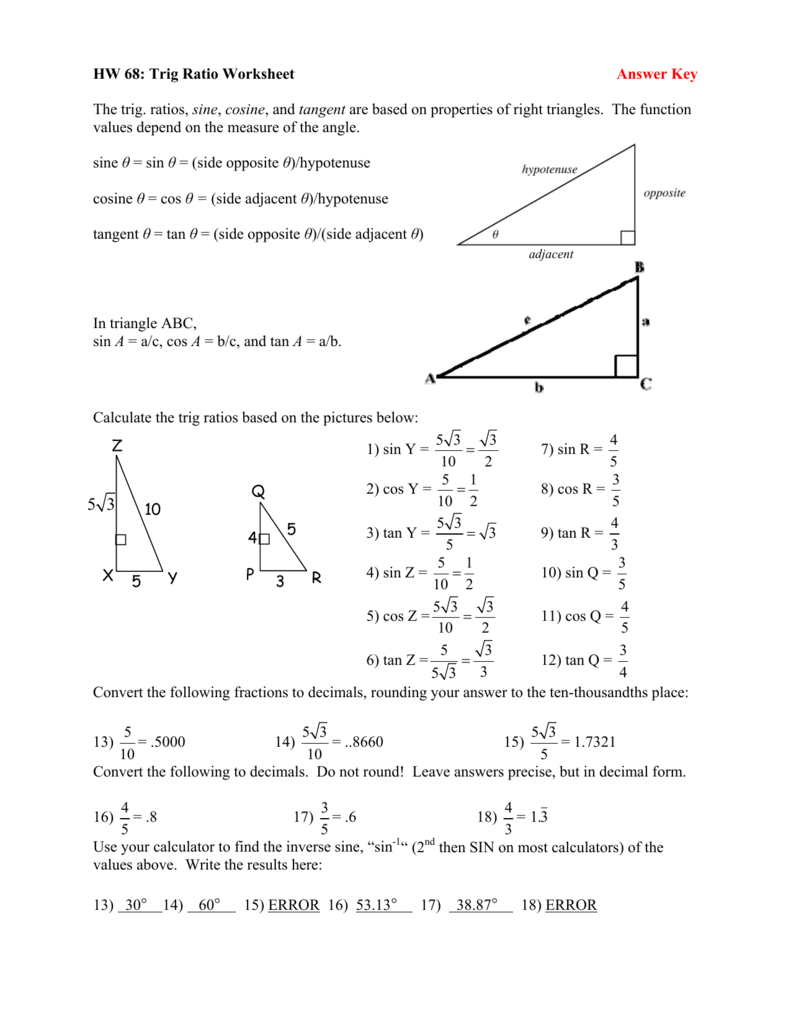
Trigonometric ratios are a fundamental concept in mathematics, and mastering them is essential for success in various fields, including physics, engineering, and computer science. In this article, we will provide a comprehensive guide on how to master the 8 basic trigonometric ratios with a simple worksheet.
What are Trigonometric Ratios?
Trigonometric ratios are relationships between the sides of a right-angled triangle. The three basic trigonometric ratios are sine (sin), cosine (cos), and tangent (tan). These ratios are defined as:
- Sine (sin): opposite side / hypotenuse
- Cosine (cos): adjacent side / hypotenuse
- Tangent (tan): opposite side / adjacent side
These three basic ratios can be used to derive five other trigonometric ratios: cosecant (csc), secant (sec), cotangent (cot), versine (ver), and coversine (cvs).
The 8 Basic Trigonometric Ratios
Here are the 8 basic trigonometric ratios, including their definitions and formulas:
- Sine (sin): opposite side / hypotenuse
- Cosine (cos): adjacent side / hypotenuse
- Tangent (tan): opposite side / adjacent side
- Cosecant (csc): hypotenuse / opposite side
- Secant (sec): hypotenuse / adjacent side
- Cotangent (cot): adjacent side / opposite side
- Versine (ver): 1 - cos
- Coversine (cvs): 1 - sin
Mastering Trigonometric Ratios with a Simple Worksheet
Now that we have reviewed the 8 basic trigonometric ratios, let’s create a simple worksheet to help you master them. Here’s a step-by-step guide on how to use the worksheet:
- Start with the basics: Begin by reviewing the definitions and formulas of the 8 trigonometric ratios.
- Practice with simple triangles: Use the worksheet to practice finding the trigonometric ratios of simple right-angled triangles.
- Use the ratios to find missing sides: Once you are comfortable finding the trigonometric ratios, use the ratios to find missing sides of right-angled triangles.
- Apply the ratios to real-world problems: Finally, apply the trigonometric ratios to real-world problems, such as finding the height of a building or the distance to a ship at sea.
Sample Worksheet

| Triangle | Angle | Sin | Cos | Tan | Csc | Sec | Cot | Ver | Cvs |
|---|---|---|---|---|---|---|---|---|---|
| 3-4-5 | 30° | 1/2 | √3/2 | 1/√3 | 2 | 2/√3 | √3 | 1/2 | 1/2 |
| 5-12-13 | 45° | 12/13 | 5/13 | 12/5 | 13/12 | 13/5 | 5/12 | 6/13 | 7/13 |
Tips and Tricks
Here are some tips and tricks to help you master the 8 basic trigonometric ratios:
- Use the unit circle: The unit circle is a powerful tool for visualizing the trigonometric ratios.
- Practice, practice, practice: The more you practice finding the trigonometric ratios, the more comfortable you will become.
- Use online resources: There are many online resources available to help you master the trigonometric ratios, including video tutorials and practice problems.
📝 Note: Practice regularly to master the 8 basic trigonometric ratios. Try to solve at least 5-10 problems every day.
By following these tips and using the simple worksheet provided, you can master the 8 basic trigonometric ratios in no time. Remember to practice regularly and apply the ratios to real-world problems to reinforce your understanding.
The ability to master the 8 basic trigonometric ratios is a fundamental skill that can benefit you in many areas of mathematics and science. With practice and dedication, you can become proficient in finding the trigonometric ratios and applying them to a wide range of problems.
What are the 8 basic trigonometric ratios?
+The 8 basic trigonometric ratios are: sine (sin), cosine (cos), tangent (tan), cosecant (csc), secant (sec), cotangent (cot), versine (ver), and coversine (cvs).
How can I master the 8 basic trigonometric ratios?
+To master the 8 basic trigonometric ratios, start by reviewing the definitions and formulas, practice finding the ratios of simple triangles, use the ratios to find missing sides, and apply the ratios to real-world problems.
What is the unit circle, and how can it help me master the 8 basic trigonometric ratios?
+The unit circle is a powerful tool for visualizing the trigonometric ratios. It can help you understand the relationships between the ratios and make it easier to find the ratios of triangles.



