Master 5 Ways to Solve Similar Right Triangles

Unlocking the Secrets of Similar Right Triangles

Right triangles are a fundamental concept in geometry, and understanding their properties is crucial for solving various mathematical problems. Similar right triangles, in particular, are a fascinating topic that can help you simplify complex calculations and unlock new problem-solving strategies. In this article, we will delve into the world of similar right triangles and explore five ways to solve them.

What are Similar Right Triangles?

Before we dive into the solutions, let’s define what similar right triangles are. Similar triangles are triangles that have the same shape but not necessarily the same size. In other words, they are identical in terms of their angles, but their side lengths can differ. Right triangles, on the other hand, are triangles with one right angle (90 degrees). When we combine these two concepts, we get similar right triangles – triangles that have the same angles (one of which is a right angle) but different side lengths.

Why are Similar Right Triangles Important?

Similar right triangles are crucial in various mathematical applications, including trigonometry, geometry, and algebra. They can help you:

• Simplify complex calculations by reducing them to simpler, more manageable problems
• Identify patterns and relationships between different triangles
• Solve problems involving proportional relationships and scaling
• Develop problem-solving strategies that can be applied to a wide range of mathematical problems

5 Ways to Solve Similar Right Triangles

Now that we’ve covered the basics, let’s explore five ways to solve similar right triangles.

Method 1: Using Similarity Statements

Similarity statements are a powerful tool for solving similar right triangles. A similarity statement is a statement that describes the relationship between two similar triangles. For example, if we have two similar right triangles, ΔABC and ΔDEF, we can write a similarity statement as:

ΔABC ~ ΔDEF

This statement tells us that the two triangles are similar, meaning they have the same angles and proportional side lengths.

📝 Note: When writing a similarity statement, make sure to include the tilde symbol (~) to indicate similarity.

Method 2: Using Proportional Relationships

Similar right triangles have proportional side lengths. This means that the ratio of the corresponding sides of the two triangles is constant. We can use this property to solve similar right triangles by setting up proportional relationships between the sides.

For example, if we have two similar right triangles, ΔABC and ΔDEF, with side lengths AB = 3, BC = 4, and AC = 5, and DE = 6, EF = 8, and DF = 10, we can set up the following proportional relationship:

AB/DE = BC/EF = AC/DF

³⁄₆ = ⁴⁄₈ = ⁵⁄₁₀

This proportional relationship tells us that the ratio of the corresponding sides of the two triangles is constant, allowing us to solve for unknown side lengths.

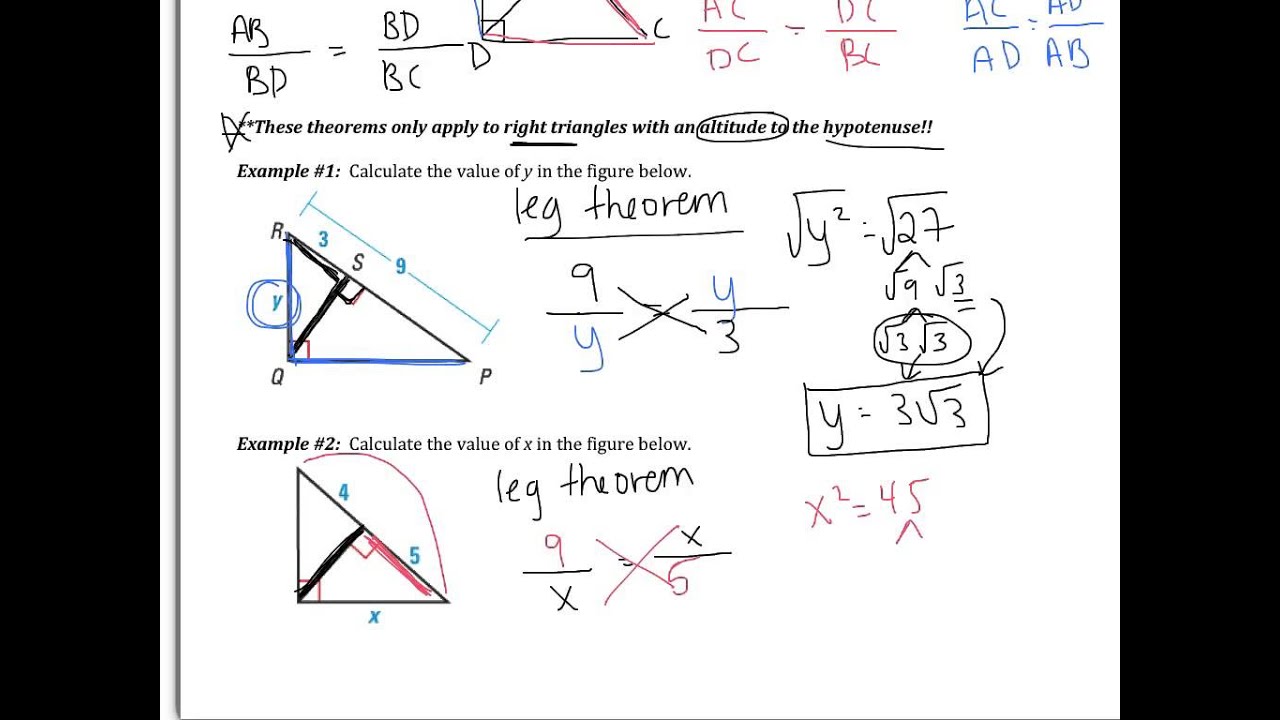
Method 3: Using the Pythagorean Theorem

The Pythagorean theorem is a fundamental concept in geometry that describes the relationship between the side lengths of a right triangle. The theorem states that:

a^2 + b^2 = c^2

where a and b are the legs of the right triangle, and c is the hypotenuse.

We can use the Pythagorean theorem to solve similar right triangles by applying it to one of the triangles and then using the resulting equation to solve for unknown side lengths.

Method 4: Using Trigonometric Ratios

Trigonometric ratios are a powerful tool for solving right triangles. We can use trigonometric ratios to solve similar right triangles by setting up equations that relate the ratios of the corresponding sides.

For example, if we have two similar right triangles, ΔABC and ΔDEF, with side lengths AB = 3, BC = 4, and AC = 5, and DE = 6, EF = 8, and DF = 10, we can set up the following trigonometric equation:

sin(∠A) = opposite side (BC) / hypotenuse (AC)

sin(∠A) = ⁴⁄₅

This equation tells us that the sine of angle A is equal to the ratio of the opposite side (BC) to the hypotenuse (AC). We can use this equation to solve for unknown angles and side lengths.

Method 5: Using the Side-Splitting Theorem

The side-splitting theorem is a useful concept for solving similar right triangles. The theorem states that if a line intersects two sides of a triangle, then it divides the triangle into two similar triangles.

We can use the side-splitting theorem to solve similar right triangles by drawing a line that intersects two sides of the triangle and then using the resulting similar triangles to solve for unknown side lengths.

Real-World Applications of Similar Right Triangles

Similar right triangles have numerous real-world applications, including:

• Architecture: Similar right triangles are used in the design of buildings, bridges, and other structures to ensure stability and balance.
• Engineering: Similar right triangles are used in the design of mechanical systems, electrical circuits, and other engineering applications.
• Physics: Similar right triangles are used to describe the motion of objects and the forces that act upon them.
• Computer Science: Similar right triangles are used in computer graphics, game development, and other computer science applications.

In conclusion, similar right triangles are a fundamental concept in geometry that can help you simplify complex calculations and unlock new problem-solving strategies. By mastering the five methods outlined in this article, you can become proficient in solving similar right triangles and apply your knowledge to a wide range of mathematical and real-world problems.

Related Terms:

• Similar polygons Worksheet
• Right triangle Similarity Theorem
• Right triangle Similarity pdf