5 Ways to Master Segment Addition Postulate
Unlocking the Secrets of Segment Addition Postulate
The segment addition postulate is a fundamental concept in geometry that can be a bit tricky to grasp at first. However, with practice and persistence, you can master this concept and take your geometry skills to the next level. In this article, we will explore five ways to help you master the segment addition postulate.
What is the Segment Addition Postulate?
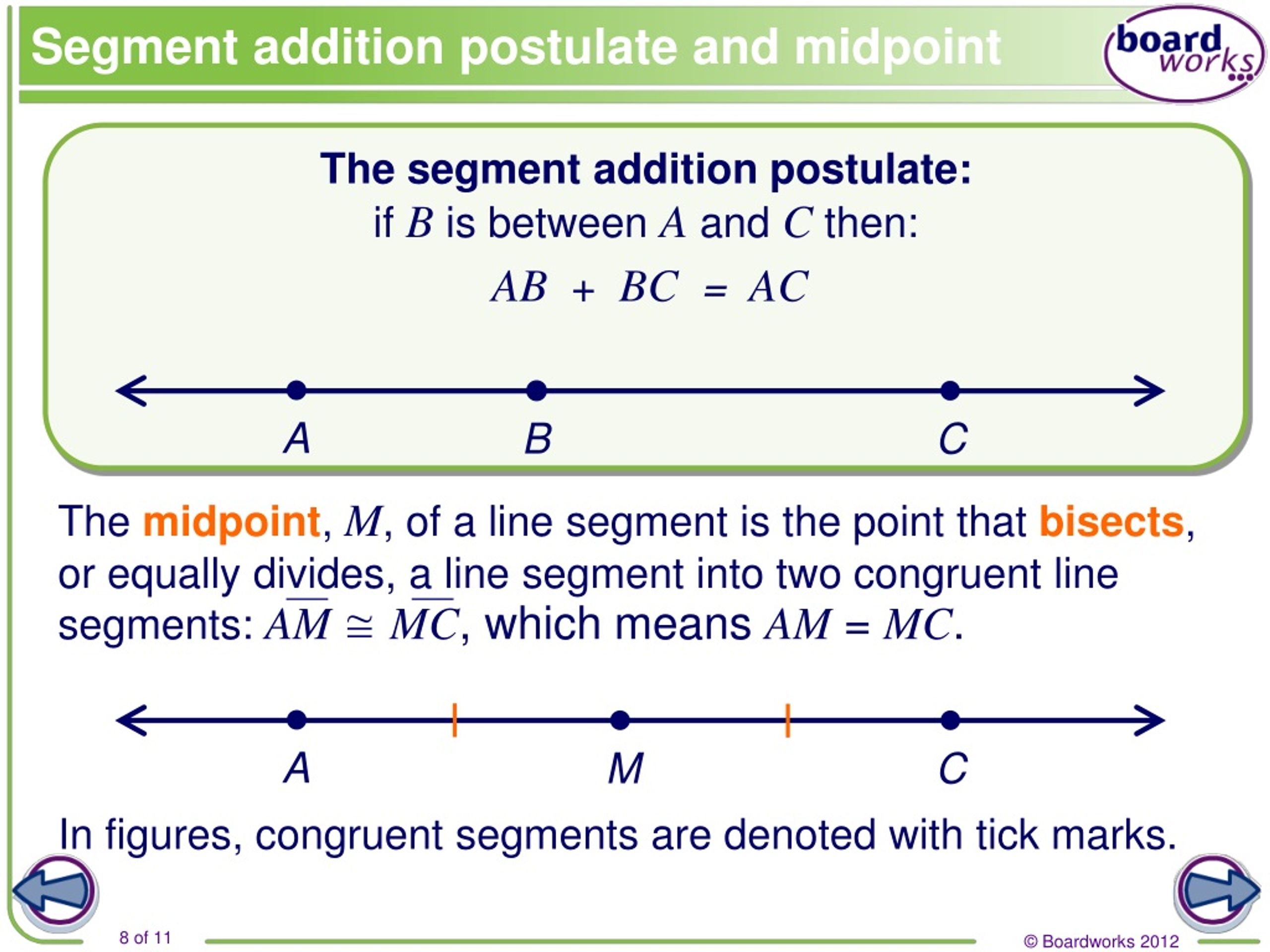
Before we dive into the five ways to master the segment addition postulate, let’s first define what it is. The segment addition postulate states that if point B is between points A and C, then the length of segment AB added to the length of segment BC is equal to the length of segment AC.
🤔 Note: This postulate is a fundamental property of geometry and is used to prove various theorems and corollaries.
1. Visualize the Concept
One of the best ways to master the segment addition postulate is to visualize it. Draw a diagram with points A, B, and C, and label the segments AB, BC, and AC. Then, use a ruler to measure the lengths of each segment. This will help you see the relationship between the segments and how they add up.
2. Practice with Real-World Examples
Another way to master the segment addition postulate is to practice with real-world examples. For instance, imagine you are a carpenter building a bookshelf. You need to measure the length of a board that will fit between two other boards. By applying the segment addition postulate, you can calculate the length of the board needed.
3. Use Algebraic Equations
The segment addition postulate can also be expressed algebraically. Let’s say the length of segment AB is x, the length of segment BC is y, and the length of segment AC is z. Then, we can write the equation:
x + y = z
This equation represents the segment addition postulate, where x and y are the lengths of the two segments that add up to z.
4. Apply the Postulate to Geometric Shapes
The segment addition postulate is not limited to just segments. It can also be applied to geometric shapes such as triangles and quadrilaterals. For example, if you have a triangle with sides AB, BC, and AC, you can use the segment addition postulate to find the length of the third side.
5. Watch Video Tutorials and Online Lessons
Finally, if you are still struggling to master the segment addition postulate, consider watching video tutorials and online lessons. There are many resources available online that can provide you with a more detailed explanation and examples of how to apply the postulate.
| Resource | Description |
|---|---|
| Khan Academy | Free online video tutorials and lessons on geometry and the segment addition postulate. |
| Mathway | Online math problem solver that can help you practice and apply the segment addition postulate. |
| Geometry Dashboard | Interactive online geometry dashboard that provides lessons, examples, and exercises on the segment addition postulate. |
In conclusion, mastering the segment addition postulate takes time and practice. By visualizing the concept, practicing with real-world examples, using algebraic equations, applying the postulate to geometric shapes, and watching video tutorials and online lessons, you can become proficient in this fundamental concept of geometry.
What is the segment addition postulate?
+The segment addition postulate states that if point B is between points A and C, then the length of segment AB added to the length of segment BC is equal to the length of segment AC.
How can I visualize the segment addition postulate?
+Draw a diagram with points A, B, and C, and label the segments AB, BC, and AC. Then, use a ruler to measure the lengths of each segment.
Can I apply the segment addition postulate to geometric shapes?
+Yes, the segment addition postulate can be applied to geometric shapes such as triangles and quadrilaterals.



