5 Ways to Solve Quadratic Equations Word Problems

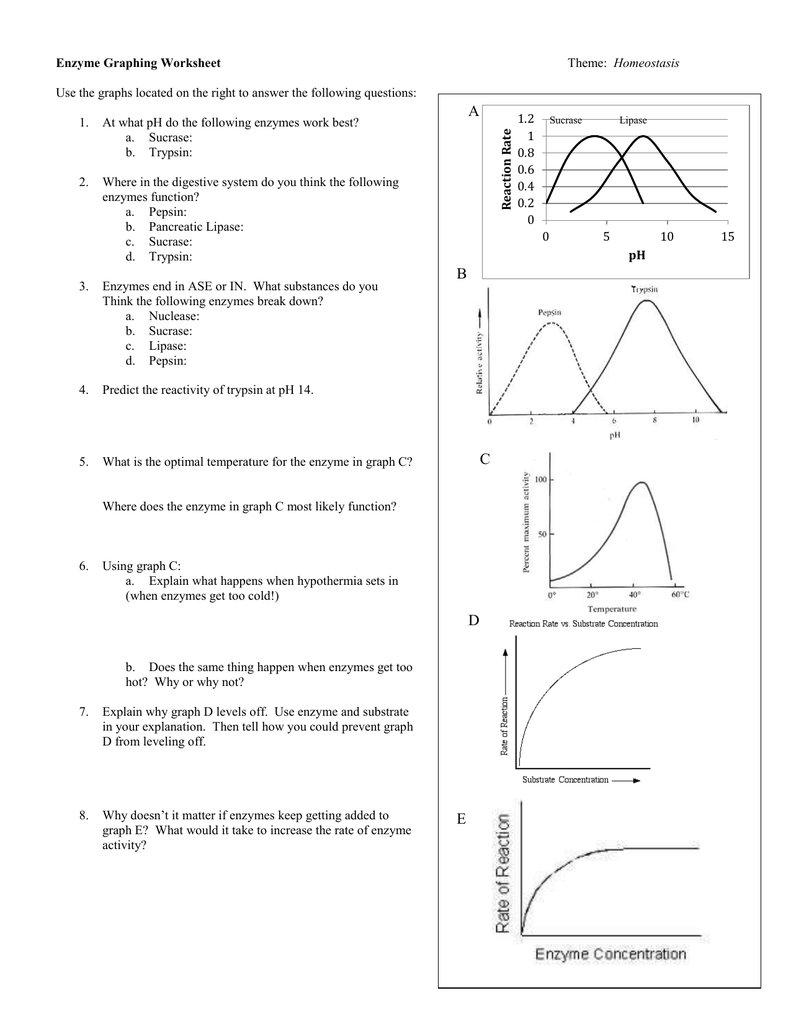
Understanding Quadratic Equations Word Problems
Quadratic equations word problems can be a daunting task for many students. These types of problems require the application of quadratic equations to real-world scenarios, making them more complex and challenging. However, with the right approach and strategies, solving quadratic equations word problems can become more manageable. In this article, we will explore five ways to solve quadratic equations word problems.
Method 1: Read and Understand the Problem
Before solving a quadratic equation word problem, it is essential to read and understand the problem thoroughly. This involves identifying the key elements of the problem, such as the variables, constants, and the relationships between them. Take your time to read the problem carefully, and make sure you understand what is being asked.
📝 Note: Underline or highlight the key elements of the problem to help you focus on the essential information.
For example, consider the following problem:
“The height of a ball thrown upward from the ground is given by the equation h(t) = -16t^2 + 32t + 1, where h is the height in feet and t is the time in seconds. Find the maximum height reached by the ball.”
In this problem, the key elements are the equation h(t) = -16t^2 + 32t + 1, the variable h (height), and the variable t (time).
Method 2: Identify the Type of Quadratic Equation
Quadratic equations can be categorized into different types, such as factorable, quadratic formula, and completing the square. Identifying the type of quadratic equation can help you choose the most suitable method for solving the problem.
- Factorable quadratic equations can be factored into the product of two binomials.
- Quadratic formula is used when the equation cannot be factored.
- Completing the square is a method used to solve quadratic equations by transforming them into perfect square trinomials.
For example, consider the following problem:
“Solve the equation x^2 + 5x + 6 = 0.”
This equation is factorable, and can be factored into (x + 3)(x + 2) = 0.
Method 3: Use the Quadratic Formula
The quadratic formula is a powerful tool for solving quadratic equations. The formula is given by:
x = (-b ± √(b^2 - 4ac)) / 2a
where a, b, and c are the coefficients of the quadratic equation.
For example, consider the following problem:
“Solve the equation x^2 + 2x + 1 = 0.”
Using the quadratic formula, we get:
x = (-(2) ± √((2)^2 - 4(1)(1))) / 2(1) x = (-2 ± √(4 - 4)) / 2 x = (-2 ± √0) / 2 x = (-2 ± 0) / 2 x = -1
Method 4: Complete the Square
Completing the square is a method used to solve quadratic equations by transforming them into perfect square trinomials. This method involves adding and subtracting a constant term to the equation to make it a perfect square trinomial.
For example, consider the following problem:
“Solve the equation x^2 + 6x + 8 = 0.”
To complete the square, we add and subtract (6⁄2)^2 = 9 to the equation:
x^2 + 6x + 9 - 9 + 8 = 0 (x + 3)^2 - 1 = 0 (x + 3)^2 = 1 x + 3 = ±√1 x = -3 ± 1
Method 5: Use Graphing to Solve Quadratic Equations
Graphing is a visual method used to solve quadratic equations. This method involves graphing the quadratic equation on a coordinate plane and finding the x-intercepts.
For example, consider the following problem:
“Solve the equation x^2 - 4x - 3 = 0.”
To solve this equation using graphing, we graph the equation on a coordinate plane and find the x-intercepts.

| x | y |
|---|---|
| -1 | 0 |
| 3 | 0 |
The x-intercepts are x = -1 and x = 3.
Conclusion
Solving quadratic equations word problems requires a combination of mathematical techniques and problem-solving strategies. By understanding the problem, identifying the type of quadratic equation, using the quadratic formula, completing the square, and graphing, you can solve quadratic equations word problems with confidence.
What is a quadratic equation?
+A quadratic equation is a polynomial equation of degree two, which means the highest power of the variable is two.
How do I identify the type of quadratic equation?
+You can identify the type of quadratic equation by looking at the coefficients and the constant term. If the equation can be factored, it is a factorable quadratic equation. If it cannot be factored, you can use the quadratic formula or complete the square.
What is the quadratic formula?
+The quadratic formula is a formula used to solve quadratic equations. It is given by x = (-b ± √(b^2 - 4ac)) / 2a, where a, b, and c are the coefficients of the quadratic equation.
Related Terms:
- Quadratic Applications Worksheet with answers