5 Ways to Master Pythagorean Theorem Geometry
Understanding the Basics of Pythagorean Theorem
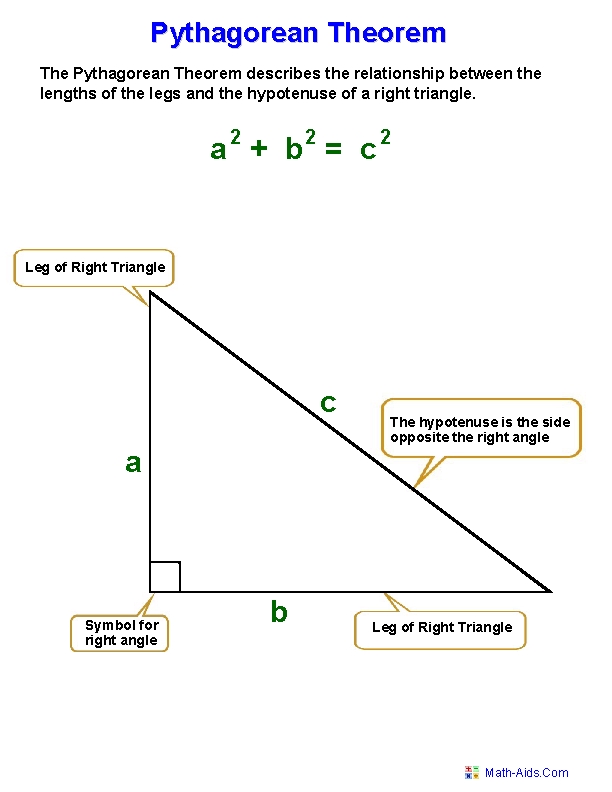
The Pythagorean Theorem is a fundamental concept in geometry that has been widely used for centuries. It states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This can be expressed mathematically as a^2 + b^2 = c^2, where a and b are the lengths of the two sides, and c is the length of the hypotenuse.
Visualizing the Theorem
To better understand the Pythagorean Theorem, it’s essential to visualize it. Imagine a right-angled triangle with two shorter sides of lengths 3 and 4. By applying the theorem, we can calculate the length of the hypotenuse, which is equal to √(3^2 + 4^2) = √(9 + 16) = √25 = 5. This means that if we have a right-angled triangle with one side of length 3 and the other of length 4, the hypotenuse will always be 5 units long.
Practical Applications of the Pythagorean Theorem
The Pythagorean Theorem has numerous practical applications in various fields, including:
- Construction: Builders use the theorem to calculate the height of buildings, the length of shadows, and the distance between objects.
- Physics: The theorem is used to calculate distances, velocities, and forces in problems involving right-angled triangles.
- Engineering: The theorem is applied in the design of bridges, roads, and other structures.
- Computer Graphics: The theorem is used to create 3D models and animations.
Mastering the Theorem with Examples
To master the Pythagorean Theorem, practice is essential. Here are a few examples to get you started:
- Example 1: In a right-angled triangle, the length of the hypotenuse is 10 units, and one of the shorter sides is 6 units. What is the length of the other shorter side?
- Example 2: A building is 15 meters tall, and the length of its shadow is 20 meters. What is the distance from the building to the point where the shadow ends?
Solutions:
- Example 1: Using the theorem, we can calculate the length of the other shorter side as √(10^2 - 6^2) = √(100 - 36) = √64 = 8 units.
- Example 2: By applying the theorem, we can calculate the distance from the building to the point where the shadow ends as √(15^2 + 20^2) = √(225 + 400) = √625 = 25 meters.
📝 Note: When solving problems involving the Pythagorean Theorem, it's essential to identify the right-angled triangle and label the sides correctly.
Tips and Tricks for Solving Problems
Here are a few tips and tricks to help you solve problems involving the Pythagorean Theorem:
- Identify the right-angled triangle: Make sure you can identify the right-angled triangle in the problem.
- Label the sides correctly: Label the sides of the triangle correctly, including the hypotenuse and the shorter sides.
- Use the theorem: Apply the theorem to solve for the unknown side length.
- Check your answers: Always check your answers to ensure they make sense in the context of the problem.
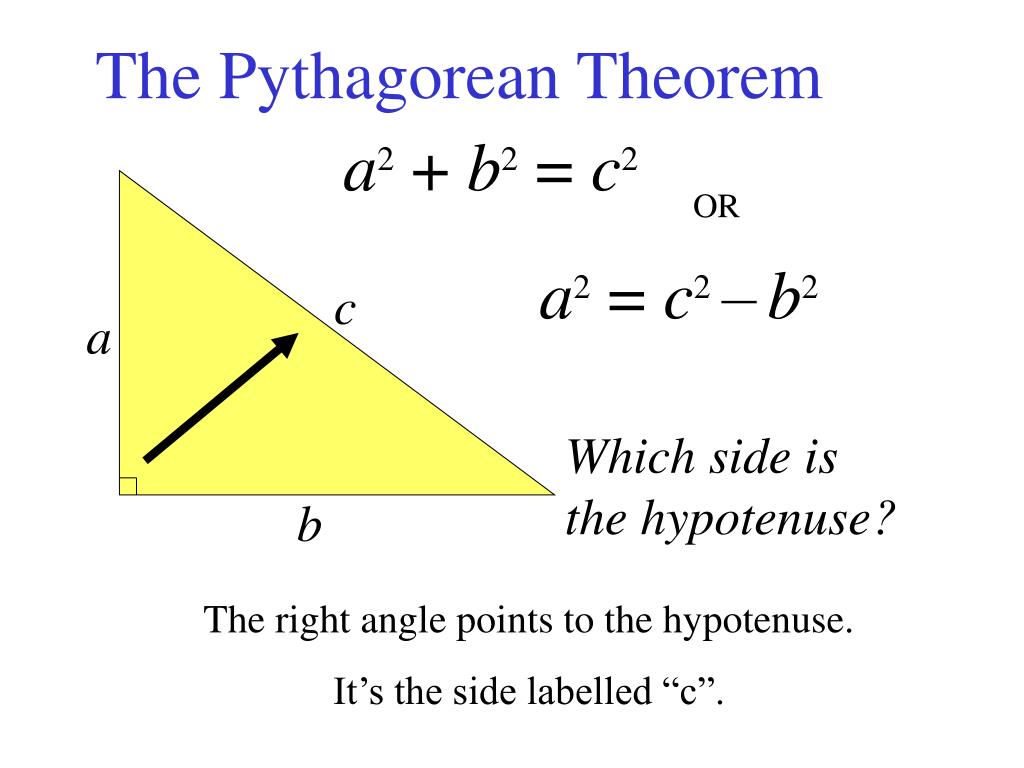
| Pythagorean Theorem Formula | a^2 + b^2 = c^2 |
|---|---|
| Variables | a, b, c |
| Description | a and b are the lengths of the shorter sides, and c is the length of the hypotenuse |
As you practice solving problems involving the Pythagorean Theorem, you’ll become more comfortable and confident in your ability to apply the theorem in a variety of situations. With persistence and dedication, you’ll master the theorem and be able to tackle even the most challenging geometry problems.
In this blog post, we’ve explored the basics of the Pythagorean Theorem, its practical applications, and provided examples and tips to help you master the theorem. We hope this information has been helpful and informative.
What is the Pythagorean Theorem?
+The Pythagorean Theorem is a mathematical concept that states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
How do I apply the Pythagorean Theorem?
+To apply the Pythagorean Theorem, identify the right-angled triangle, label the sides correctly, and use the theorem to solve for the unknown side length.
What are some practical applications of the Pythagorean Theorem?
+The Pythagorean Theorem has numerous practical applications in various fields, including construction, physics, engineering, and computer graphics.