Adding Fractions with Unlike Denominators Made Easy

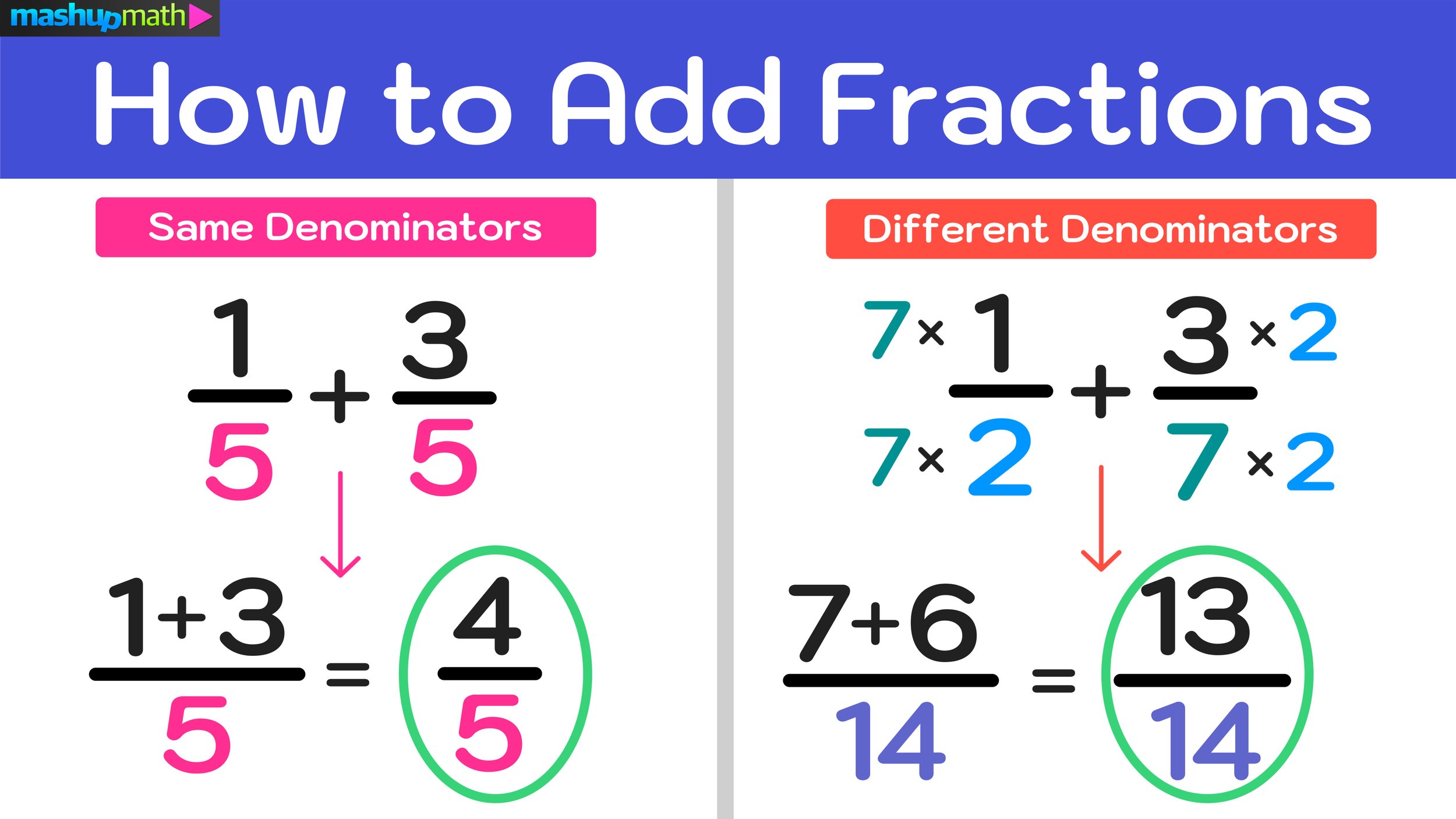
Adding Fractions with Unlike Denominators: A Step-by-Step Guide

Adding fractions with unlike denominators can be a challenging task for many students. However, with a clear understanding of the concept and a few simple steps, it can become a breeze. In this article, we will explore the concept of adding fractions with unlike denominators and provide a step-by-step guide on how to do it.

What are Unlike Denominators?

Unlike denominators refer to fractions that have different denominators. For example, ¹⁄₄ and ¹⁄₆ are fractions with unlike denominators because they have different denominators, 4 and 6. When adding fractions with unlike denominators, we need to find a common denominator first.

Step 1: Find the Least Common Multiple (LCM)

To add fractions with unlike denominators, we need to find the least common multiple (LCM) of the two denominators. The LCM is the smallest number that is a multiple of both denominators.

For example, let’s say we want to add ¹⁄₄ and ¹⁄₆. The multiples of 4 are 4, 8, 12, 16, and so on. The multiples of 6 are 6, 12, 18, 24, and so on. Therefore, the LCM of 4 and 6 is 12.

Step 2: Convert Each Fraction to Have the LCM as the Denominator

Once we have found the LCM, we need to convert each fraction to have the LCM as the denominator. We do this by multiplying the numerator and denominator of each fraction by the necessary multiple.

Using the example above, we can convert ¹⁄₄ to have a denominator of 12 by multiplying the numerator and denominator by 3:

¹⁄₄ = (1 x 3) / (4 x 3) = ³⁄₁₂

Similarly, we can convert ¹⁄₆ to have a denominator of 12 by multiplying the numerator and denominator by 2:

¹⁄₆ = (1 x 2) / (6 x 2) = ²⁄₁₂

Step 3: Add the Fractions

Now that both fractions have the same denominator, we can add them by adding the numerators and keeping the denominator the same:

³⁄₁₂ + ²⁄₁₂ = (3 + 2) / 12 = ⁵⁄₁₂

Example 2: Adding Fractions with Unlike Denominators

Let’s say we want to add ²⁄₅ and ³⁄₈. To do this, we need to find the LCM of 5 and 8.

The multiples of 5 are 5, 10, 15, 20, 25, 30, 35, 40, and so on. The multiples of 8 are 8, 16, 24, 32, 40, and so on. Therefore, the LCM of 5 and 8 is 40.

Next, we convert each fraction to have a denominator of 40:

²⁄₅ = (2 x 8) / (5 x 8) = ¹⁶⁄₄₀

³⁄₈ = (3 x 5) / (8 x 5) = ¹⁵⁄₄₀

Finally, we add the fractions:

¹⁶⁄₄₀ + ¹⁵⁄₄₀ = (16 + 15) / 40 = ³¹⁄₄₀

Tips and Tricks

• Always find the LCM of the denominators before adding fractions with unlike denominators.
• Use the LCM to convert each fraction to have the same denominator.
• When adding fractions with unlike denominators, make sure to add the numerators and keep the denominator the same.

📝 Note: When adding fractions with unlike denominators, it's essential to find the LCM of the denominators. This ensures that we can convert each fraction to have the same denominator, making it possible to add them.

Adding Fractions with Unlike Denominators: A Real-World Example

Let’s say you have ¹⁄₄ cup of sugar and ¹⁄₆ cup of flour. You want to know how much you have in total. To do this, you need to add the fractions.

First, find the LCM of 4 and 6, which is 12. Then, convert each fraction to have a denominator of 12:

¹⁄₄ = (1 x 3) / (4 x 3) = ³⁄₁₂

¹⁄₆ = (1 x 2) / (6 x 2) = ²⁄₁₂

Finally, add the fractions:

³⁄₁₂ + ²⁄₁₂ = (3 + 2) / 12 = ⁵⁄₁₂

Therefore, you have ⁵⁄₁₂ cup of sugar and flour in total.

Conclusion

Adding fractions with unlike denominators is a straightforward process that requires finding the LCM of the denominators and converting each fraction to have the same denominator. By following these steps, you can easily add fractions with unlike denominators. Remember to always find the LCM and convert each fraction to have the same denominator.