Dilation Worksheet 8Th Grade
Understanding Dilation in 8th Grade Math
Dilation is a fundamental concept in geometry that involves changing the size of a figure while maintaining its shape. In 8th grade math, students learn to apply dilation to various geometric figures, including polygons, circles, and three-dimensional objects. In this article, we will explore the concept of dilation, its types, and provide a comprehensive dilation worksheet for 8th grade students.
What is Dilation?
Dilation is a transformation that changes the size of a figure by scaling it up or down. It is a type of similarity transformation, which means that the shape of the original figure remains the same, but its size changes. Dilation can be represented mathematically using a scale factor, which is a ratio of the lengths of corresponding sides of the original and dilated figures.
Types of Dilation
There are two main types of dilation:
- Enlargement: An enlargement is a dilation that increases the size of a figure. It is represented by a scale factor greater than 1.
- Reduction: A reduction is a dilation that decreases the size of a figure. It is represented by a scale factor less than 1.
How to Perform Dilation
To perform a dilation, you need to know the center of dilation, the scale factor, and the original figure. The center of dilation is the point from which the dilation is performed. The scale factor determines the amount of enlargement or reduction.
Here are the steps to perform a dilation:
- Identify the center of dilation.
- Determine the scale factor.
- Draw a line from the center of dilation to each vertex of the original figure.
- Measure the distance from the center of dilation to each vertex of the original figure.
- Multiply the distance by the scale factor to find the corresponding distance in the dilated figure.
- Draw the dilated figure using the new distances.
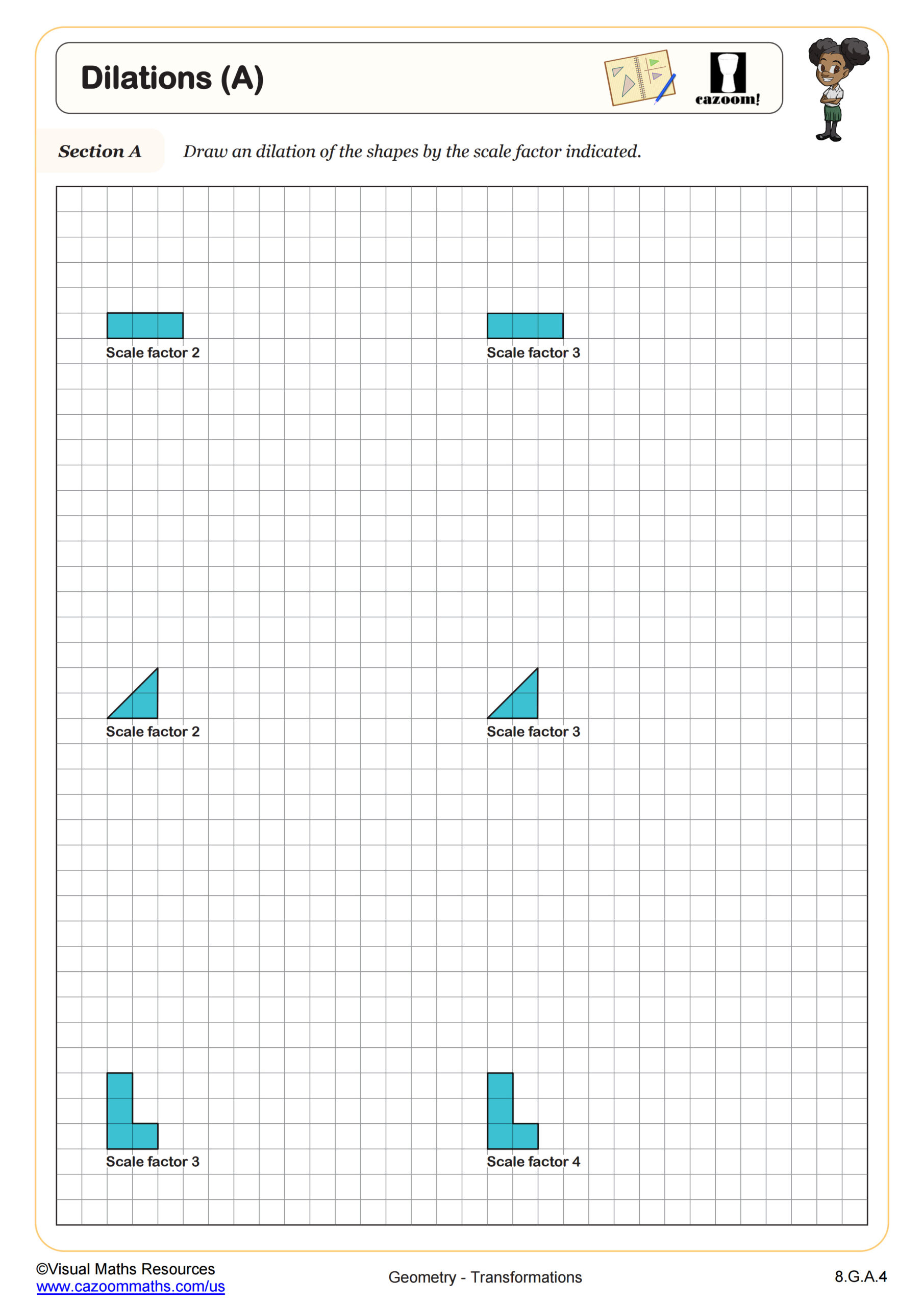
Dilation Worksheet for 8th Grade
Here is a comprehensive dilation worksheet for 8th grade students:
Section 1: Multiple Choice Questions
- What is the scale factor of a dilation that enlarges a figure by 50%? a) 1.5 b) 2 c) 3 d) 4
Answer: a) 1.5
- Which of the following is an example of a reduction? a) Enlarging a figure by 200% b) Reducing a figure by 50% c) Translating a figure 5 units to the right d) Rotating a figure 90 degrees
Answer: b) Reducing a figure by 50%
Section 2: Short Answer Questions
- What is the center of dilation in the diagram below?
[Insert diagram of a dilation with center marked]
Answer: The center of dilation is point A.
- If a dilation has a scale factor of 2, what is the ratio of the corresponding sides of the original and dilated figures?
Answer: The ratio is 1:2.
Section 3: Problem-Solving Questions
- Dilate the figure below by a scale factor of 3 with the center of dilation at point A.
[Insert diagram of a figure with center marked]
Answer: [Insert dilated figure]
- A dilation with a scale factor of 0.5 is performed on a triangle with side lengths 6, 8, and 10. What are the side lengths of the dilated triangle?
Answer: The side lengths of the dilated triangle are 3, 4, and 5.
Important Notes
📝 Note: Remember to always label the center of dilation and the scale factor when performing a dilation.
📝 Note: A dilation can be performed using a graph paper or a coordinate plane.
Conclusion
Dilation is an essential concept in geometry that involves changing the size of a figure while maintaining its shape. By understanding the types of dilation, how to perform dilation, and practicing with worksheets, 8th grade students can master this concept and apply it to various geometric figures.
What is the difference between enlargement and reduction?
+
An enlargement increases the size of a figure, while a reduction decreases the size of a figure.
How do you find the scale factor of a dilation?
+
The scale factor is the ratio of the lengths of corresponding sides of the original and dilated figures.
Can a dilation be performed on a three-dimensional object?
+
Yes, a dilation can be performed on a three-dimensional object, but it requires a different approach than dilating a two-dimensional figure.
Related Terms:
- Teacher synergy llc
- Khan Academy
- IXL
- BrainPOP
- Udacity
- Duolingo



