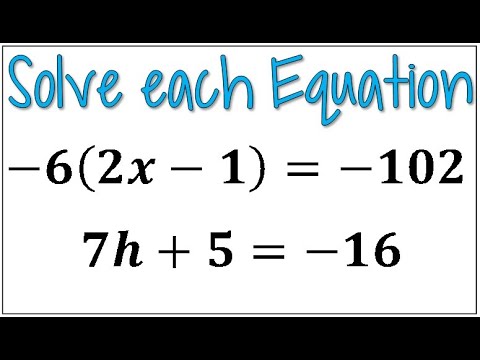5 Ways to Master Parallel Lines and Transversals

Understanding Parallel Lines and Transversals
Parallel lines and transversals are fundamental concepts in geometry, and mastering them is crucial for solving various problems in mathematics and real-life applications. In this article, we will explore five ways to master parallel lines and transversals, along with examples and illustrations to help you understand these concepts better.
1. Learn the Basic Definitions
To start with, it’s essential to understand the basic definitions of parallel lines and transversals.
- Parallel Lines: Two lines are said to be parallel if they lie in the same plane and do not intersect, no matter how far they are extended. In other words, parallel lines never meet or cross each other.
- Transversals: A transversal is a line that intersects two or more lines, which may be parallel or non-parallel. When a transversal intersects two parallel lines, it forms pairs of congruent corresponding angles, alternate interior angles, and alternate exterior angles.

2. Identify Corresponding Angles, Alternate Interior Angles, and Alternate Exterior Angles
When a transversal intersects two parallel lines, it forms several pairs of congruent angles. These include:
- Corresponding Angles: These are angles that are in the same relative position on each line, with the transversal intersecting the lines. Corresponding angles are always congruent.
- Alternate Interior Angles: These are angles that are on opposite sides of the transversal, but inside the parallel lines. Alternate interior angles are always congruent.
- Alternate Exterior Angles: These are angles that are on opposite sides of the transversal, but outside the parallel lines. Alternate exterior angles are always congruent.
📝 Note: It's essential to identify these angles correctly to solve problems involving parallel lines and transversals.
3. Practice Solving Problems
The best way to master parallel lines and transversals is to practice solving problems. Here are a few examples:
- If two parallel lines are intersected by a transversal, and one angle measures 60°, find the measure of the corresponding angle.
- In a diagram, ∠A and ∠B are alternate interior angles. If ∠A measures 45°, find the measure of ∠B.
- Two parallel lines are intersected by a transversal. If the alternate exterior angles measure 30° and 150°, find the measure of the corresponding angle.
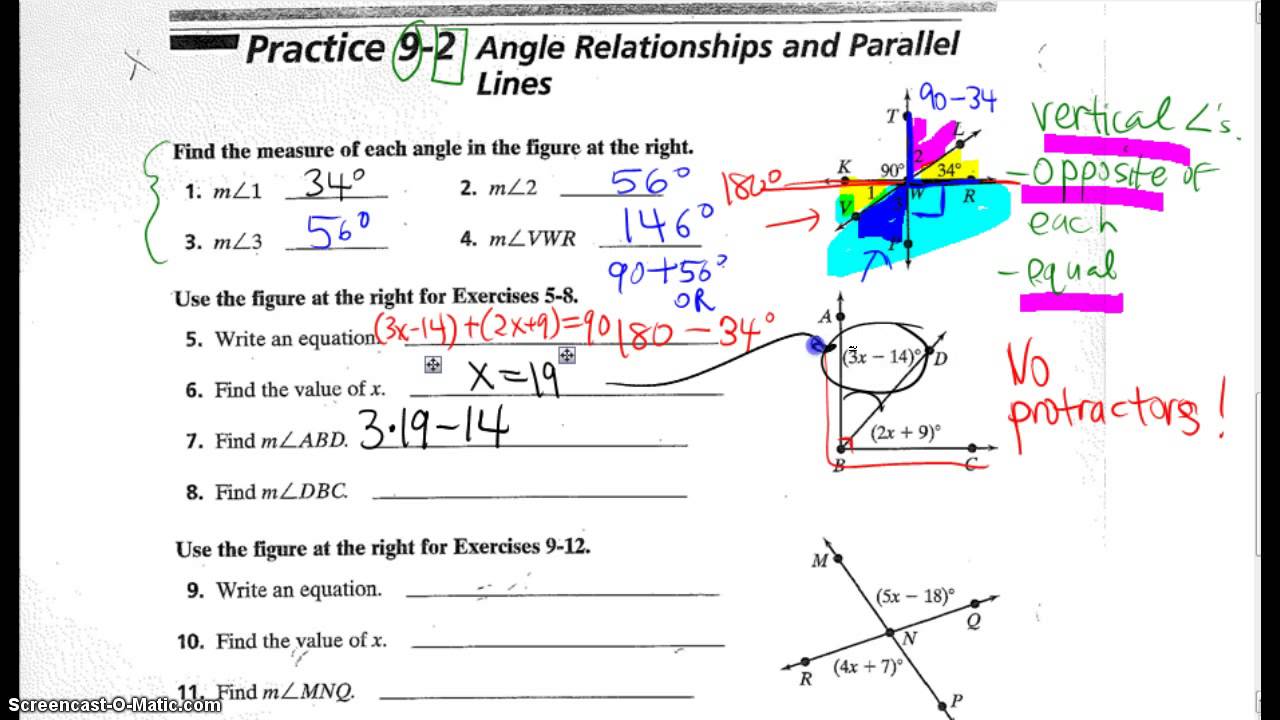
4. Use Visual Aids and Diagrams
Visual aids and diagrams can help you better understand parallel lines and transversals. Here are a few tips:
- Draw diagrams to illustrate the problem.
- Use a ruler or straightedge to draw parallel lines.
- Use a protractor to measure angles.

| Angle Type | Description |
|---|---|
| Corresponding Angles | Angles that are in the same relative position on each line |
| Alternate Interior Angles | Angles that are on opposite sides of the transversal, but inside the parallel lines |
| Alternate Exterior Angles | Angles that are on opposite sides of the transversal, but outside the parallel lines |
5. Watch Video Tutorials and Online Lessons
There are many online resources available to help you master parallel lines and transversals. Here are a few suggestions:
- Khan Academy: Offers video tutorials and practice exercises on parallel lines and transversals.
- Mathway: Provides online lessons and practice problems on parallel lines and transversals.
- IXL: Offers interactive practice exercises on parallel lines and transversals.
By following these five ways, you can master parallel lines and transversals and improve your skills in geometry. Remember to practice regularly and use visual aids and diagrams to help you understand these concepts better.
To summarize, mastering parallel lines and transversals requires a combination of understanding the basic definitions, identifying corresponding angles, alternate interior angles, and alternate exterior angles, practicing solving problems, using visual aids and diagrams, and watching video tutorials and online lessons.