Angle Relationships Puzzle Worksheet Answers
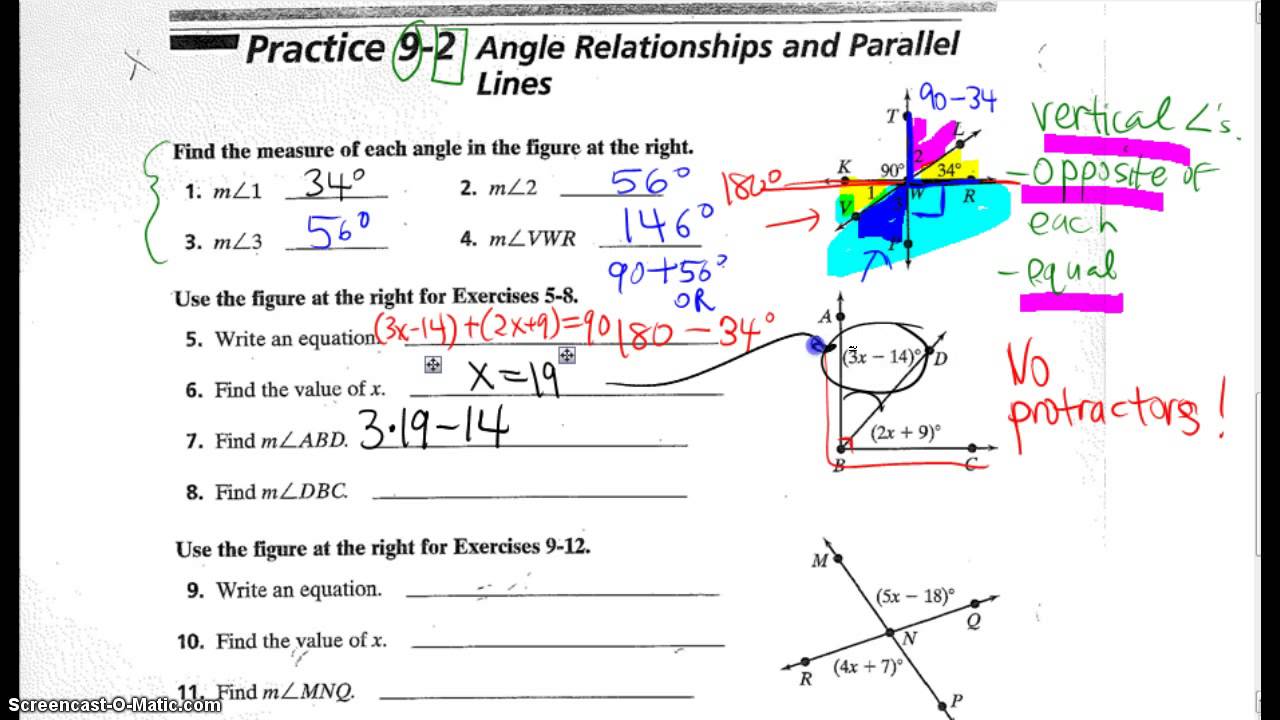
Understanding Angle Relationships
Angle relationships are a fundamental concept in geometry, and understanding them is crucial for solving various puzzles and problems. In this worksheet, we will explore different types of angle relationships, including complementary, supplementary, vertical, and corresponding angles.
Complementary Angles
Complementary angles are two angles whose sum is 90 degrees. These angles do not have to be adjacent or form a linear pair.
📝 Note: Complementary angles are like two pieces of a puzzle that fit together to form a right angle.
Example 1: Find the measure of the complementary angle of 30 degrees.
- Since the sum of complementary angles is 90 degrees, we can set up the equation: 30 + x = 90
- Solving for x, we get: x = 60
Answer: The complementary angle of 30 degrees is 60 degrees.
Supplementary Angles
Supplementary angles are two angles whose sum is 180 degrees. Like complementary angles, supplementary angles do not have to be adjacent or form a linear pair.
📝 Note: Supplementary angles are like two pieces of a puzzle that fit together to form a straight angle.
Example 2: Find the measure of the supplementary angle of 120 degrees.
- Since the sum of supplementary angles is 180 degrees, we can set up the equation: 120 + x = 180
- Solving for x, we get: x = 60
Answer: The supplementary angle of 120 degrees is 60 degrees.
Vertical Angles
Vertical angles are two non-adjacent angles formed by two intersecting lines. These angles are always equal in measure.
📝 Note: Vertical angles are like two identical pieces of a puzzle that fit together perfectly.
Example 3: If ∠A and ∠B are vertical angles, and ∠A measures 45 degrees, what is the measure of ∠B?
- Since vertical angles are equal, we can conclude that ∠B also measures 45 degrees.
Answer: The measure of ∠B is 45 degrees.
Corresponding Angles
Corresponding angles are two non-adjacent angles formed by a transversal line that intersects two parallel lines. These angles are always equal in measure.
📝 Note: Corresponding angles are like two identical pieces of a puzzle that fit together perfectly, even when they are far apart.
Example 4: If ∠A and ∠B are corresponding angles, and ∠A measures 60 degrees, what is the measure of ∠B?
- Since corresponding angles are equal, we can conclude that ∠B also measures 60 degrees.
Answer: The measure of ∠B is 60 degrees.
| Angle Relationship | Definition | Example |
|---|---|---|
| Complementary Angles | Two angles whose sum is 90 degrees. | 30 + 60 = 90 |
| Supplementary Angles | Two angles whose sum is 180 degrees. | 120 + 60 = 180 |
| Vertical Angles | Two non-adjacent angles formed by two intersecting lines. | ∠A = ∠B = 45 degrees |
| Corresponding Angles | Two non-adjacent angles formed by a transversal line that intersects two parallel lines. | ∠A = ∠B = 60 degrees |
By understanding and applying these angle relationships, you can solve various puzzles and problems with ease.
In this worksheet, we have explored different types of angle relationships, including complementary, supplementary, vertical, and corresponding angles. By mastering these concepts, you can improve your problem-solving skills and become more confident in your ability to tackle challenging puzzles and problems.
Remember, practice makes perfect! Try solving more angle relationship puzzles to reinforce your understanding of these concepts.
What is the difference between complementary and supplementary angles?
+Complementary angles have a sum of 90 degrees, while supplementary angles have a sum of 180 degrees.
Are vertical angles always equal in measure?
+Yes, vertical angles are always equal in measure.
What is the definition of corresponding angles?
+Corresponding angles are two non-adjacent angles formed by a transversal line that intersects two parallel lines.