Solve Multistep Equations with Confidence and Accuracy

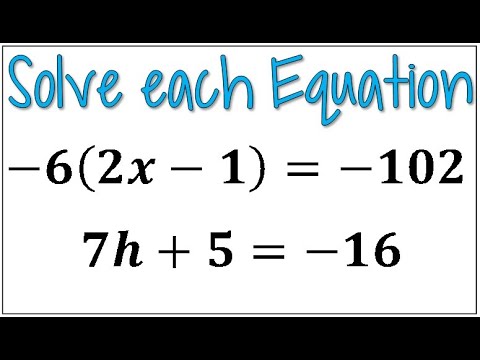
Breaking Down Complex Equations into Manageable Steps

Solving multistep equations can be a daunting task, especially for students who are new to algebra. However, with a clear understanding of the steps involved and a few simple strategies, you can become proficient in solving these types of equations with confidence and accuracy. In this article, we will walk you through a step-by-step guide on how to solve multistep equations, and provide you with tips and tricks to help you along the way.

Understanding the Basics of Multistep Equations

Before we dive into the nitty-gritty of solving multistep equations, let’s first understand what they are. Multistep equations are algebraic equations that require more than one step to solve. They often involve a combination of addition, subtraction, multiplication, and division, and may include variables and constants on both sides of the equation.

Step 1: Simplify the Equation

The first step in solving a multistep equation is to simplify the equation by combining like terms. This involves adding or subtracting constants and variables on the same side of the equation.

Example:

2x + 5 = 11

To simplify this equation, we can start by combining the constants on the right-hand side:

2x = 11 - 5 2x = 6

Step 2: Isolate the Variable

The next step is to isolate the variable (in this case, x) by getting rid of the coefficient (the number that is multiplied by the variable). To do this, we can divide both sides of the equation by the coefficient.

Example:

2x = 6

To isolate x, we can divide both sides of the equation by 2:

x = 6 ÷ 2 x = 3

Step 3: Check Your Solution

Once you have isolated the variable, it’s essential to check your solution by plugging it back into the original equation.

Example:

2x + 5 = 11

Substituting x = 3 into the equation, we get:

2(3) + 5 = 11 6 + 5 = 11 11 = 11

This confirms that our solution is correct.

Tips and Tricks for Solving Multistep Equations

Here are some additional tips and tricks to help you solve multistep equations with confidence and accuracy:

• Read the equation carefully: Take your time to read the equation carefully, and make sure you understand what is required.
• Break down the equation: Break down the equation into smaller, manageable steps. This will help you to focus on one step at a time.
• Use inverse operations: Use inverse operations to isolate the variable. For example, if the equation involves addition, use subtraction to isolate the variable.
• Check your solution: Always check your solution by plugging it back into the original equation.

🔍 Note: Make sure to check your solution carefully, as a small mistake can lead to an incorrect solution.

Common Mistakes to Avoid

Here are some common mistakes to avoid when solving multistep equations:

• Not combining like terms: Failing to combine like terms can lead to an incorrect solution.
• Not isolating the variable: Failing to isolate the variable can lead to an incorrect solution.
• Not checking your solution: Failing to check your solution can lead to an incorrect solution.

📝 Note: Take your time to check your solution carefully, as a small mistake can lead to an incorrect solution.

Conclusion

Solving multistep equations requires patience, persistence, and attention to detail. By following the steps outlined in this article, and using the tips and tricks provided, you can become proficient in solving these types of equations with confidence and accuracy. Remember to always check your solution carefully, and avoid common mistakes that can lead to an incorrect solution.