5 Ways to Master Right Triangle Trig

Understanding the Fundamentals of Right Triangle Trigonometry

Right triangle trigonometry is a fundamental concept in mathematics and physics, and mastering it can open doors to more advanced math concepts and problem-solving skills. In this article, we will explore the basics of right triangle trigonometry, discuss common misconceptions, and provide tips and strategies for mastering it.

1. SoH-Cah-Toa: The Ultimate Right Triangle Trig Formula

SoH-Cah-Toa is a mnemonic device that helps you remember the relationships between the angles and side lengths of a right triangle. It stands for:

• Sine = Opposite over Hypotenuse
• Cosine = Adjacent over Hypotenuse
• Tangent = Opposite over Adjacent

This formula is essential for solving right triangle trig problems. By remembering SoH-Cah-Toa, you can easily find the sine, cosine, and tangent of any angle in a right triangle.

Example:

In a right triangle with a 30° angle, the opposite side is 3 inches and the hypotenuse is 6 inches. What is the sine of the 30° angle?

Using SoH-Cah-Toa, we get:

sin(30°) = Opposite / Hypotenuse = 3 / 6 = 0.5

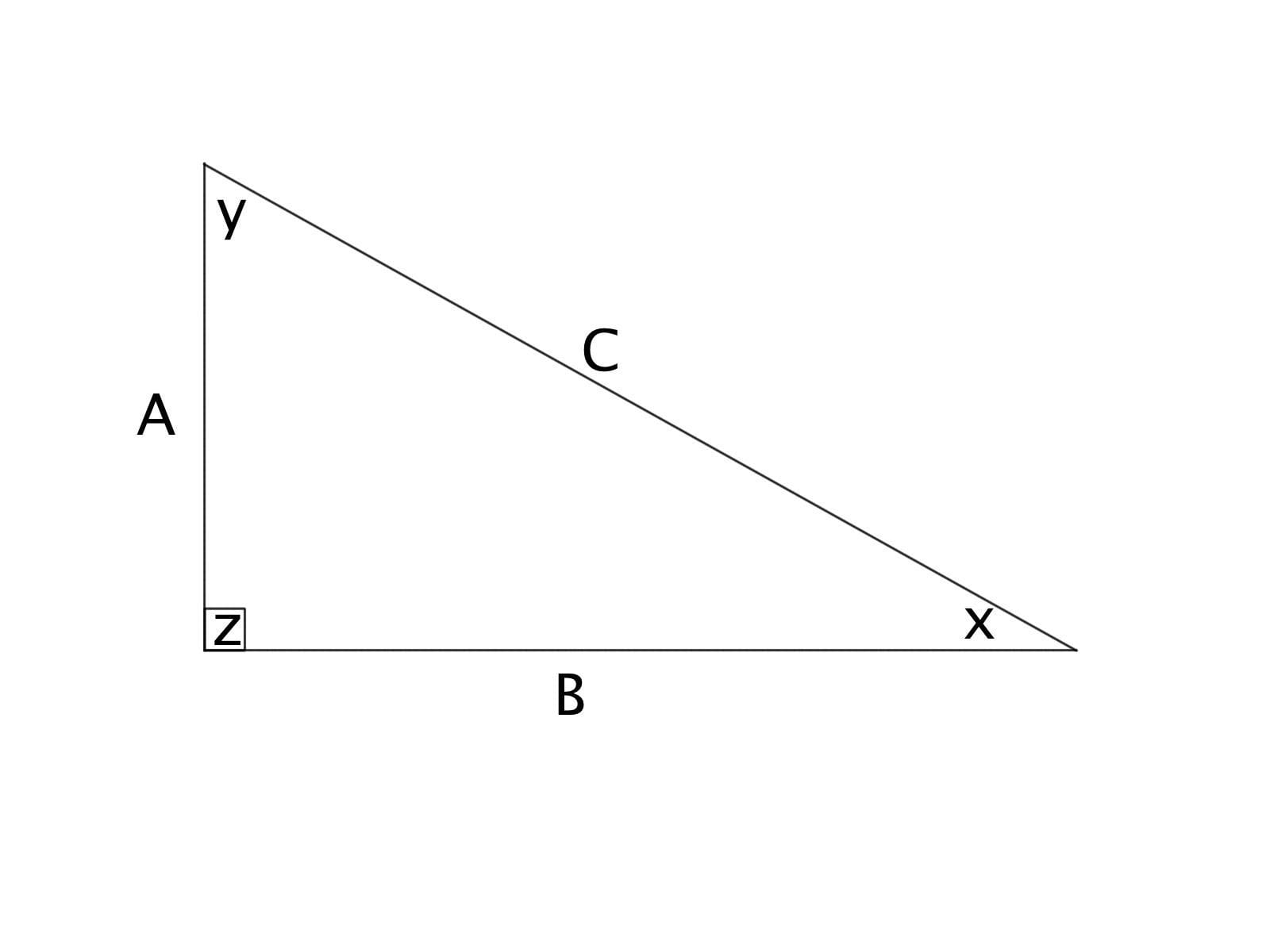
2. Visualizing Right Triangles

Visualizing right triangles is crucial for mastering trigonometry. By drawing diagrams and labeling the angles and side lengths, you can better understand the relationships between them.

Here are a few tips for visualizing right triangles:

• Use a unit circle: Draw a unit circle with a radius of 1 and label the angles and side lengths. This will help you visualize the relationships between the angles and side lengths.
• Draw diagrams: Draw diagrams of right triangles with different angles and side lengths. Label the angles and side lengths, and use SoH-Cah-Toa to find the sine, cosine, and tangent of each angle.
• Use graph paper: Use graph paper to draw right triangles and visualize the relationships between the angles and side lengths.

Example:

Draw a right triangle with a 45° angle and label the angles and side lengths. Use SoH-Cah-Toa to find the sine, cosine, and tangent of the 45° angle.

Using SoH-Cah-Toa, we get:

sin(45°) = Opposite / Hypotenuse = 3 / 6 = 0.5 cos(45°) = Adjacent / Hypotenuse = 3 / 6 = 0.5 tan(45°) = Opposite / Adjacent = 3 / 3 = 1

3. Mastering Trigonometric Identities

Trigonometric identities are equations that relate the sine, cosine, and tangent of an angle. Mastering these identities can help you simplify complex trigonometric expressions and solve problems more efficiently.

Here are a few common trigonometric identities:

• Pythagorean identity: sin^2(x) + cos^2(x) = 1
• Sum and difference formulas: sin(a + b) = sin(a)cos(b) + cos(a)sin(b) cos(a + b) = cos(a)cos(b) - sin(a)sin(b) tan(a + b) = (tan(a) + tan(b)) / (1 - tan(a)tan(b))

Example:

Simplify the expression: sin(2x)cos(x) + cos(2x)sin(x)

Using the sum and difference formulas, we get:

sin(2x)cos(x) + cos(2x)sin(x) = sin(2x + x) = sin(3x)

4. Solving Right Triangle Trig Problems

Now that you’ve mastered SoH-Cah-Toa and trigonometric identities, it’s time to practice solving right triangle trig problems.

Here are a few tips for solving right triangle trig problems:

• Read the problem carefully: Read the problem carefully and identify the given information and the unknown quantities.
• Draw a diagram: Draw a diagram of the right triangle and label the angles and side lengths.
• Use SoH-Cah-Toa: Use SoH-Cah-Toa to find the sine, cosine, and tangent of each angle.
• Use trigonometric identities: Use trigonometric identities to simplify complex expressions and solve the problem.

Example:

In a right triangle, the length of the hypotenuse is 10 inches and the length of the adjacent side is 6 inches. What is the length of the opposite side?

Using SoH-Cah-Toa, we get:

sin(x) = Opposite / Hypotenuse = Opposite / 10

Using the Pythagorean identity, we get:

cos(x) = Adjacent / Hypotenuse = 6 / 10 cos^2(x) = 36 / 100 sin^2(x) = 1 - cos^2(x) = 1 - ³⁶⁄₁₀₀ = ⁶⁴⁄₁₀₀ sin(x) = sqrt(⁶⁴⁄₁₀₀) = ⁸⁄₁₀

Opposite = sin(x) x Hypotenuse = (⁸⁄₁₀) x 10 = 8 inches

5. Practicing with Real-World Applications

Finally, practicing with real-world applications can help you master right triangle trigonometry.

Here are a few examples of real-world applications:

• Physics and engineering: Right triangle trigonometry is used to solve problems in physics and engineering, such as finding the force of friction on an inclined plane or the stress on a beam.
• Navigation and surveying: Right triangle trigonometry is used in navigation and surveying to find the distance and direction between two points.
• Computer graphics: Right triangle trigonometry is used in computer graphics to create 3D models and animations.

By practicing with real-world applications, you can develop a deeper understanding of right triangle trigonometry and its relevance to real-world problems.

📝 Note: Mastering right triangle trigonometry takes time and practice. Be patient and persistent, and don't be afraid to ask for help when you need it.

In conclusion, mastering right triangle trigonometry requires a combination of understanding the fundamentals, practicing with real-world applications, and mastering trigonometric identities. By following these tips and strategies, you can become proficient in right triangle trigonometry and solve complex problems with ease.

Related Terms:

• Right Triangle Trigonometry Review Worksheet
• Find the missing angles worksheet
• Kuta Software Right Triangle Trigonometry
• Trigonometry Finding missing sides Worksheet