Graphing Rational Functions Made Easy with Practice Worksheets
Understanding Rational Functions
Rational functions are a fundamental concept in algebra and are used to model real-world phenomena, such as population growth, electrical circuits, and economics. A rational function is a ratio of two polynomials, where the numerator and denominator are polynomials, and the denominator is non-zero. In this article, we will explore the basics of rational functions, how to graph them, and provide practice worksheets to help you master the concept.
Types of Rational Functions
There are several types of rational functions, including:
- Proper Rational Functions: The degree of the numerator is less than the degree of the denominator.
- Improper Rational Functions: The degree of the numerator is greater than or equal to the degree of the denominator.
- Linear Rational Functions: The numerator and denominator are both linear.
Graphing Rational Functions
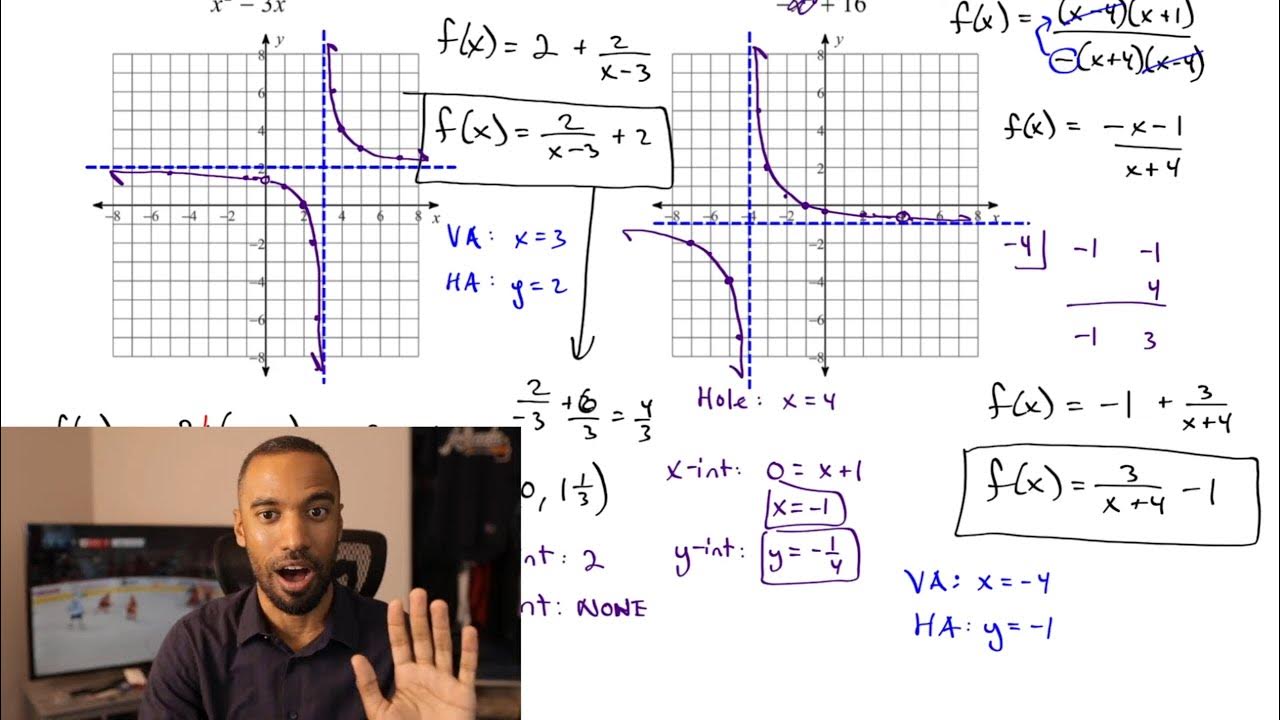
Graphing rational functions can be challenging, but with practice, you can become proficient. Here are the steps to graph a rational function:
- Find the x-intercepts: Set the numerator equal to zero and solve for x.
- Find the y-intercept: Evaluate the function at x = 0.
- Find the vertical asymptotes: Set the denominator equal to zero and solve for x.
- Find the horizontal asymptotes: Compare the degrees of the numerator and denominator.
- Graph the function: Plot the x-intercepts, y-intercept, vertical asymptotes, and horizontal asymptotes on a coordinate plane.
📝 Note: When graphing rational functions, it's essential to identify the vertical asymptotes, as they can help you determine the behavior of the function.
Practice Worksheets
Here are some practice worksheets to help you master graphing rational functions:
Worksheet 1: Graphing Rational Functions

| Function | x-intercepts | y-intercept | Vertical Asymptotes | Horizontal Asymptotes |
|---|---|---|---|---|
| 1 / (x + 2) | -2 | 1⁄2 | x = -2 | y = 0 |
| (x - 1) / (x + 3) | 1 | -1⁄3 | x = -3 | y = 1 |
| (x^2 + 1) / (x^2 - 4) | None | 1⁄4 | x = ±2 | y = 1 |
Worksheet 2: Identifying Vertical Asymptotes
| Function | Vertical Asymptotes |
|---|---|
| 1 / (x - 2) | x = 2 |
| (x + 1) / (x^2 - 9) | x = ±3 |
| (x^2 - 4) / (x - 2) | x = 2 |
Worksheet 3: Graphing Improper Rational Functions
| Function | x-intercepts | y-intercept | Vertical Asymptotes | Horizontal Asymptotes |
|---|---|---|---|---|
| (x^2 + 1) / (x + 1) | -1 | 1 | x = -1 | y = x |
| (x^3 - 2x^2 + x - 1) / (x^2 - 1) | 1, -1 | 1 | x = ±1 | y = x - 1 |
Conclusion
Graphing rational functions can seem daunting, but with practice, you can become proficient. Remember to identify the x-intercepts, y-intercept, vertical asymptotes, and horizontal asymptotes to graph a rational function. Use the practice worksheets provided to help you master the concept.
What is a rational function?
+A rational function is a ratio of two polynomials, where the numerator and denominator are polynomials, and the denominator is non-zero.
How do I graph a rational function?
+To graph a rational function, find the x-intercepts, y-intercept, vertical asymptotes, and horizontal asymptotes, and plot them on a coordinate plane.
What is the difference between a proper and improper rational function?
+A proper rational function has a numerator with a degree less than the degree of the denominator, while an improper rational function has a numerator with a degree greater than or equal to the degree of the denominator.