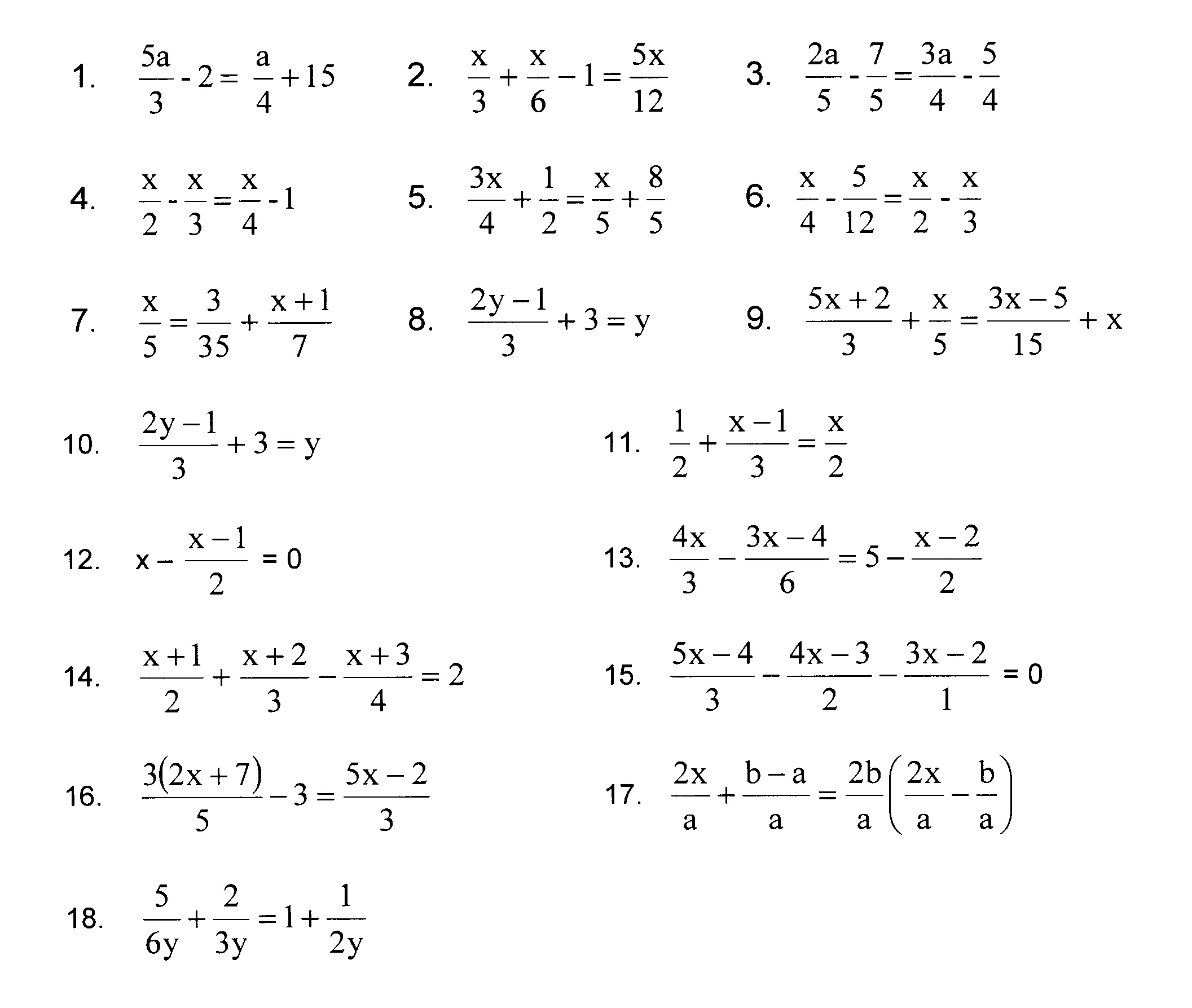Multiply and Divide Scientific Notation Made Easy

Multiplying and Dividing Scientific Notation: A Simplified Approach
Scientific notation is a compact way of expressing very large or very small numbers using the form a × 10^n, where ‘a’ is a number between 1 and 10, and ‘n’ is an integer. This notation system is widely used in mathematics, physics, and engineering to simplify complex calculations and make them more manageable.
One of the most significant advantages of scientific notation is that it allows us to perform arithmetic operations like multiplication and division quickly and accurately. In this article, we will focus on multiplying and dividing numbers in scientific notation, providing step-by-step instructions and examples to make the process crystal clear.
Multiplying Numbers in Scientific Notation
Multiplying numbers in scientific notation involves multiplying the coefficients (the ‘a’ part) and adding the exponents (the ‘n’ part). Here’s the general formula:
a × 10^n × b × 10^m = (a × b) × 10^(n+m)
Let’s break this down with an example:
Example 1: Multiply 4.2 × 10^3 and 2.5 × 10^2.
- Multiply the coefficients: 4.2 × 2.5 = 10.5
- Add the exponents: 3 + 2 = 5
- Combine the results: 10.5 × 10^5
To simplify this further, we can express 10.5 as 1.05 × 10, so the final answer becomes:
1.05 × 10^6
📝 Note: When multiplying numbers in scientific notation, it's essential to ensure that the coefficient (the 'a' part) remains between 1 and 10. If the result exceeds 10, you can adjust the coefficient and exponent accordingly, as shown in the example above.
Dividing Numbers in Scientific Notation
Dividing numbers in scientific notation involves dividing the coefficients and subtracting the exponents. Here’s the general formula:
(a × 10^n) ÷ (b × 10^m) = (a ÷ b) × 10^(n-m)
Let’s explore this with an example:
Example 2: Divide 3.6 × 10^4 by 1.8 × 10^2.
- Divide the coefficients: 3.6 ÷ 1.8 = 2
- Subtract the exponents: 4 - 2 = 2
- Combine the results: 2 × 10^2
📝 Note: When dividing numbers in scientific notation, make sure to perform the division operation carefully to avoid errors. You can always simplify the result further by adjusting the coefficient and exponent if necessary.
Real-World Applications
Scientific notation is used extensively in various fields, including physics, chemistry, and engineering. Here are a few examples of how multiplying and dividing numbers in scientific notation can be applied in real-world scenarios:
- Astronomy: When calculating the distances between celestial bodies, scientists often use scientific notation to express vast distances, such as the distance between stars or galaxies.
- Medicine: In medical research, scientists may use scientific notation to express the concentration of a particular substance in a solution, such as the concentration of a medication in a patient’s bloodstream.
- Engineering: Engineers often use scientific notation to express large quantities, such as the weight of a building or the length of a bridge.

| Operation | Scientific Notation Formula | Example |
|---|---|---|
| Multiplication | a × 10^n × b × 10^m = (a × b) × 10^(n+m) | 4.2 × 10^3 × 2.5 × 10^2 = 1.05 × 10^6 |
| Division | (a × 10^n) ÷ (b × 10^m) = (a ÷ b) × 10^(n-m) | 3.6 × 10^4 ÷ 1.8 × 10^2 = 2 × 10^2 |
In conclusion, multiplying and dividing numbers in scientific notation is a straightforward process that requires attention to detail and a basic understanding of the underlying math concepts. By following the formulas and guidelines outlined in this article, you’ll be able to perform these operations with ease and confidence.
What is scientific notation, and why is it used?
+Scientific notation is a way of expressing very large or very small numbers using the form a × 10^n, where ‘a’ is a number between 1 and 10, and ‘n’ is an integer. It’s used to simplify complex calculations and make them more manageable in mathematics, physics, and engineering.
How do I multiply numbers in scientific notation?
+To multiply numbers in scientific notation, multiply the coefficients (the ‘a’ part) and add the exponents (the ‘n’ part). Ensure that the coefficient remains between 1 and 10.
How do I divide numbers in scientific notation?
+To divide numbers in scientific notation, divide the coefficients and subtract the exponents. Perform the division operation carefully to avoid errors.
Related Terms:
- Multiplying scientific notation Worksheet pdf
- Scientific notation Multiplication Worksheet