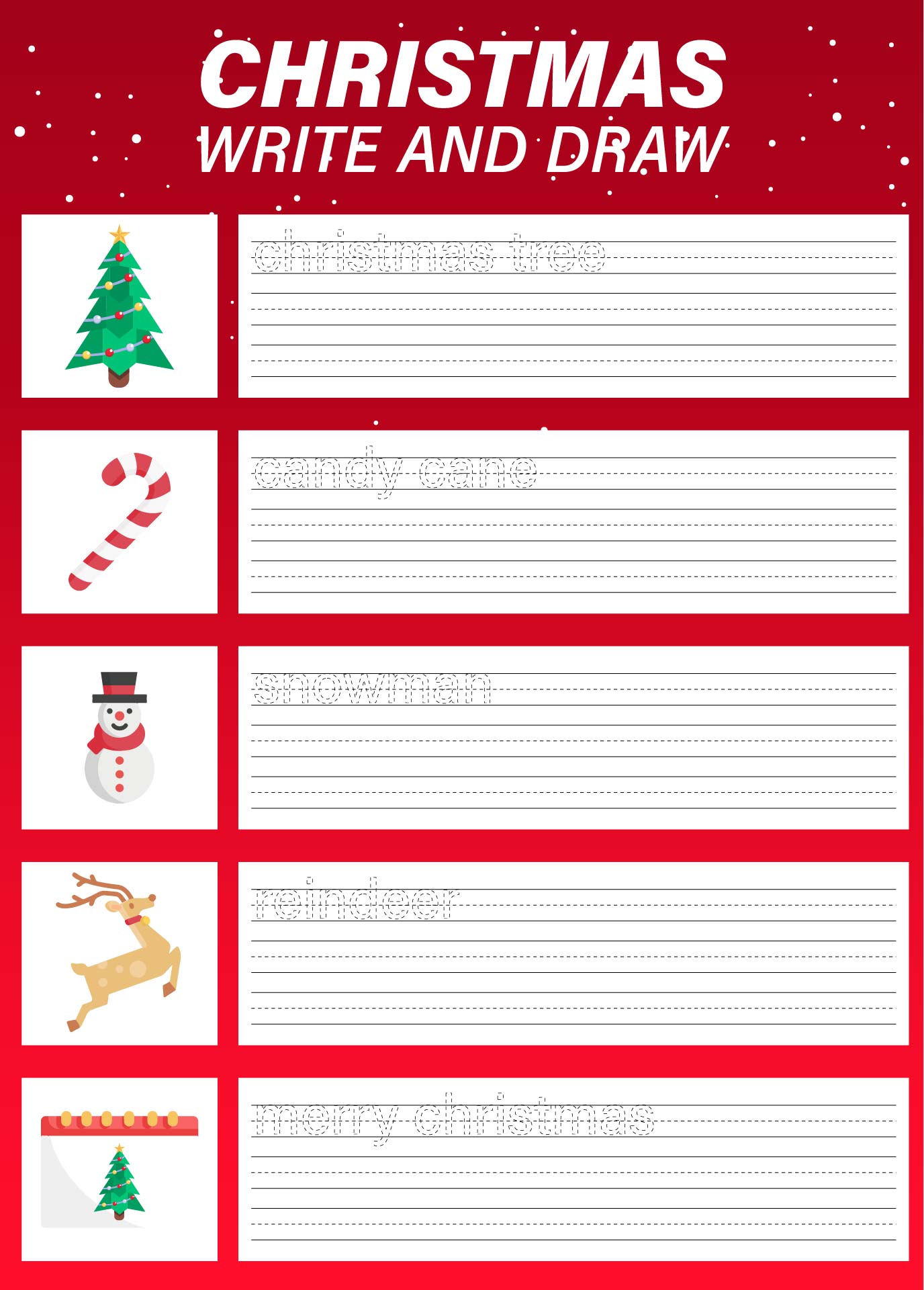
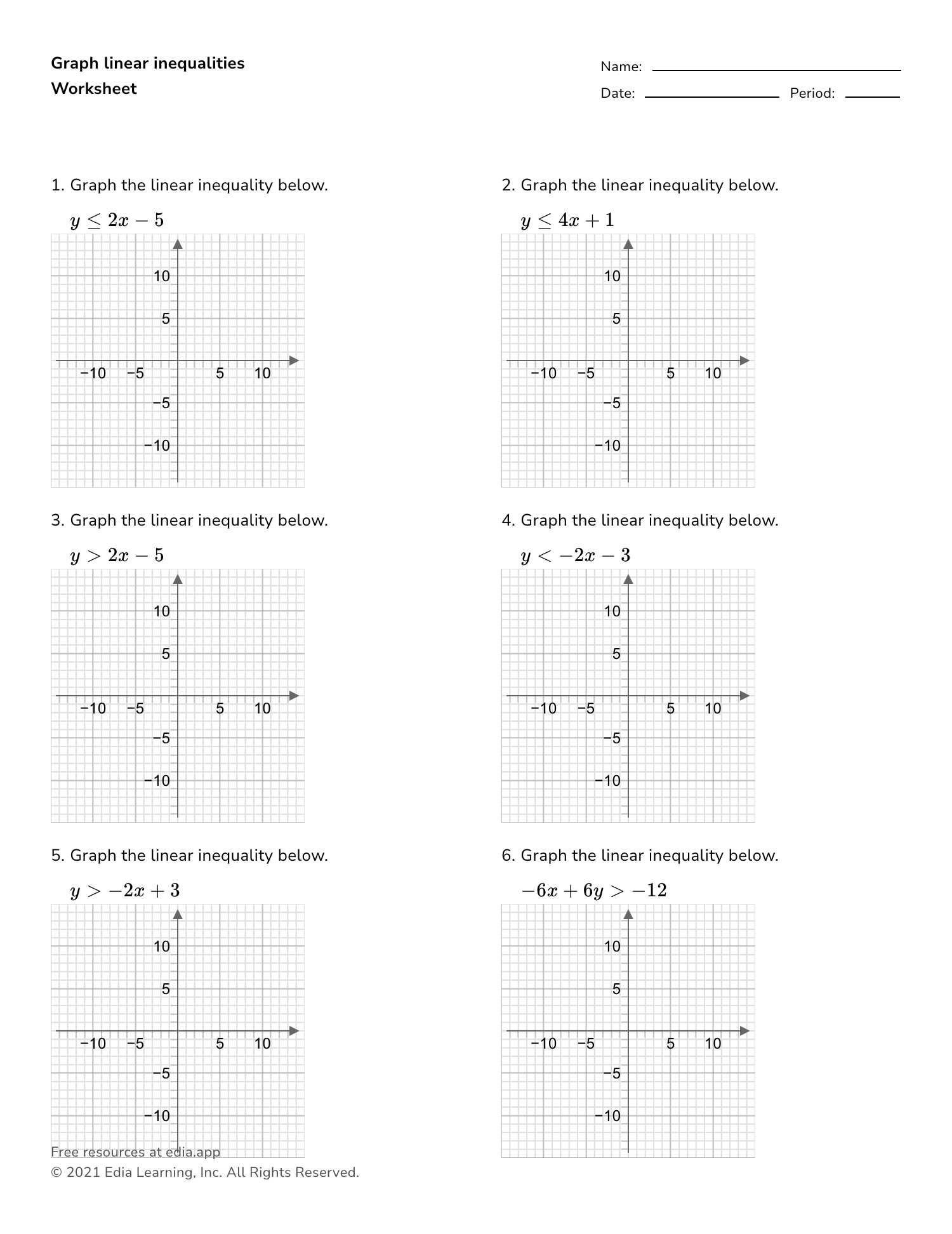
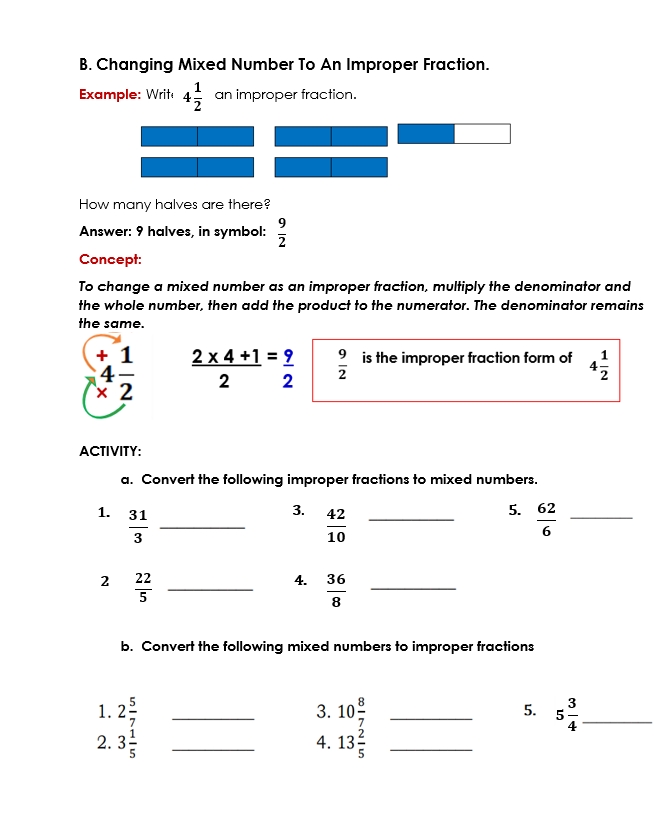
Simplifying Algebra: Equivalent Expressions Made Easy

Unlocking the Secrets of Algebra: Equivalent Expressions
Algebra can be a daunting subject for many students, but with the right approach, it can become a breeze. One of the fundamental concepts in algebra is equivalent expressions, which is essential for simplifying and solving equations. In this article, we will delve into the world of equivalent expressions, explore their importance, and provide a step-by-step guide on how to simplify them.
What are Equivalent Expressions?
Equivalent expressions are algebraic expressions that have the same value for all possible values of the variable(s) involved. In other words, two expressions are equivalent if they represent the same relationship between the variables, regardless of the order or arrangement of the terms. Equivalent expressions are essential in algebra because they allow us to simplify complex equations, solve systems of equations, and model real-world problems.
Why are Equivalent Expressions Important?
Equivalent expressions are crucial in algebra because they enable us to:
- Simplify complex equations: By recognizing equivalent expressions, we can simplify complex equations by combining like terms, canceling out common factors, and rearranging terms.
- Solve systems of equations: Equivalent expressions help us to solve systems of equations by allowing us to substitute one expression for another, making it easier to find the solution.
- Model real-world problems: Equivalent expressions enable us to model real-world problems using algebraic equations, which is essential in various fields such as physics, engineering, and economics.
Step-by-Step Guide to Simplifying Equivalent Expressions
Simplifying equivalent expressions involves a series of steps that help us to rewrite an expression in a more manageable form. Here’s a step-by-step guide:
- Combine like terms: Combine all like terms, which are terms that have the same variable(s) with the same exponent(s).
- Cancel out common factors: Cancel out any common factors that appear in both the numerator and denominator of a fraction.
- Rearrange terms: Rearrange the terms to simplify the expression.
- Use the distributive property: Use the distributive property to expand and simplify expressions.
- Check for errors: Always check your work to ensure that the simplified expression is equivalent to the original expression.
📝 Note: When simplifying equivalent expressions, it's essential to check your work to avoid errors. Use a calculator or substitute values into the original expression to verify that the simplified expression is equivalent.
Examples of Equivalent Expressions
Here are a few examples of equivalent expressions:
| Original Expression | Simplified Expression |
|---|---|
| 2x + 5x | 7x |
| x^2 + 3x - 2x | x^2 + x |
| 3(2x + 1) | 6x + 3 |
Common Mistakes to Avoid
When working with equivalent expressions, here are some common mistakes to avoid:
- Forgetting to combine like terms: Always combine like terms to simplify the expression.
- Canceling out terms that are not common factors: Be careful when canceling out terms to ensure that they are common factors.
- Rearranging terms incorrectly: Rearrange terms carefully to avoid changing the meaning of the expression.
Conclusion
Simplifying equivalent expressions is a fundamental concept in algebra that requires practice and patience. By following the step-by-step guide outlined in this article, you’ll become proficient in recognizing and simplifying equivalent expressions. Remember to always check your work and avoid common mistakes to ensure that you’re working with equivalent expressions.
What is the difference between an expression and an equation?
+An expression is a collection of variables, constants, and mathematical operations, whereas an equation is a statement that says two expressions are equal.
How do I know if two expressions are equivalent?
+Two expressions are equivalent if they have the same value for all possible values of the variable(s) involved. You can check this by substituting values into both expressions and verifying that they produce the same result.
What is the distributive property, and how is it used in simplifying equivalent expressions?
+The distributive property states that a single term can be distributed over multiple terms inside parentheses. It’s used in simplifying equivalent expressions by expanding and simplifying expressions.
Related Terms:
- Teacher synergy llc
- Khan Academy
- IXL
- BrainPOP
- Udacity
- Duolingo