Solving Multi Step Equations with Fractions Made Easy
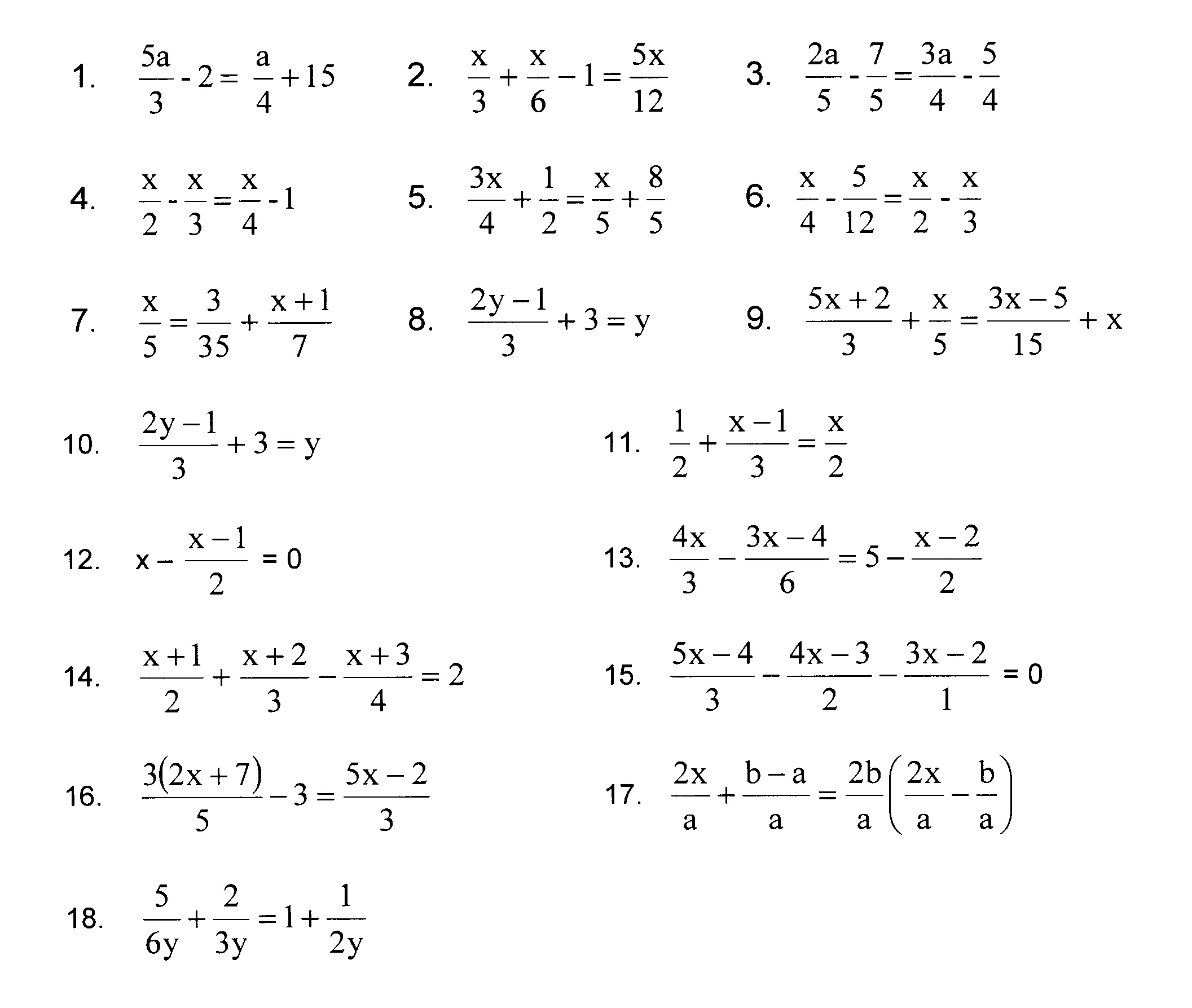
Unlocking the Secrets of Multi-Step Equations with Fractions
When it comes to solving multi-step equations with fractions, many students feel overwhelmed and unsure of where to start. However, with the right strategies and techniques, these types of equations can be tackled with ease. In this post, we’ll break down the steps to solve multi-step equations with fractions and provide you with the confidence to tackle even the most complex problems.
Understanding the Basics
Before we dive into solving multi-step equations with fractions, let’s review the basics. A multi-step equation is an equation that requires more than one step to solve. These equations often involve fractions, decimals, or percentages, and require a combination of operations to isolate the variable.
Key Concepts:
- Like terms: Terms that have the same variable raised to the same power.
- Inverse operations: Operations that “undo” each other, such as addition and subtraction, or multiplication and division.
- Order of operations: A set of rules that dictate the order in which operations should be performed.
Step 1: Simplify the Equation
The first step in solving a multi-step equation with fractions is to simplify the equation. This involves combining like terms, eliminating any parentheses, and simplifying any fractions.
Example:
Simplify the equation: 2x + 3⁄4 = 5⁄6
- Combine like terms: 2x = 5⁄6 - 3⁄4
- Eliminate parentheses: 2x = 5⁄6 - 3⁄4
- Simplify fractions: 2x = 10⁄12 - 9⁄12
- Combine like terms: 2x = 1⁄12
Step 2: Isolate the Variable
Once the equation is simplified, the next step is to isolate the variable. This involves using inverse operations to get the variable alone on one side of the equation.
Example:
Isolate the variable in the equation: 2x = 1⁄12
- Divide both sides by 2: x = 1⁄24
Step 3: Solve for the Variable
Now that the variable is isolated, the final step is to solve for the variable. This involves simplifying the fraction and expressing the answer in simplest form.
Example:
Solve for x in the equation: x = 1⁄24
- Simplify the fraction: x = 1⁄24
Tips and Tricks:
- Check your work: Always check your work by plugging the solution back into the original equation.
- Use inverse operations: Use inverse operations to isolate the variable and solve for the unknown value.
- Simplify fractions: Simplify fractions by dividing both the numerator and denominator by the greatest common divisor.
Common Mistakes to Avoid
When solving multi-step equations with fractions, there are several common mistakes to avoid. These include:
- Forgetting to simplify fractions: Failing to simplify fractions can lead to incorrect solutions.
- Using the wrong order of operations: Using the wrong order of operations can result in incorrect solutions.
- Not checking work: Failing to check work can lead to incorrect solutions.
🔍 Note: Always check your work by plugging the solution back into the original equation to ensure accuracy.
Real-World Applications
Multi-step equations with fractions have many real-world applications, including:
- Science: Multi-step equations are used in scientific formulas to describe the relationships between variables.
- Finance: Multi-step equations are used in financial calculations to determine interest rates and investment returns.
- Engineering: Multi-step equations are used in engineering to design and optimize systems.
| Concept | Definition | Example |
|---|---|---|
| Like terms | Terms that have the same variable raised to the same power. | 2x + 3x = 5x |
| Inverse operations | Operations that "undo" each other. | Addition and subtraction, or multiplication and division. |
| Order of operations | A set of rules that dictate the order in which operations should be performed. | PEMDAS (Parentheses, Exponents, Multiplication and Division, and Addition and Subtraction) |
By following these steps and tips, you’ll be able to solve multi-step equations with fractions with ease. Remember to simplify the equation, isolate the variable, and solve for the variable. With practice and patience, you’ll become a pro at solving multi-step equations with fractions.
In conclusion, solving multi-step equations with fractions requires a combination of strategies and techniques. By understanding the basics, simplifying the equation, isolating the variable, and solving for the variable, you’ll be able to tackle even the most complex problems. Remember to check your work, use inverse operations, and simplify fractions to ensure accuracy.
What is a multi-step equation?
+A multi-step equation is an equation that requires more than one step to solve.
How do I simplify a fraction?
+To simplify a fraction, divide both the numerator and denominator by the greatest common divisor.
What is the order of operations?
+The order of operations is a set of rules that dictate the order in which operations should be performed. The acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, and Addition and Subtraction) is commonly used to remember the order of operations.
Related Terms:
- teacher synergy llc
- Khan Academy
- IXL
- BrainPOP
- Udacity
- Duolingo



