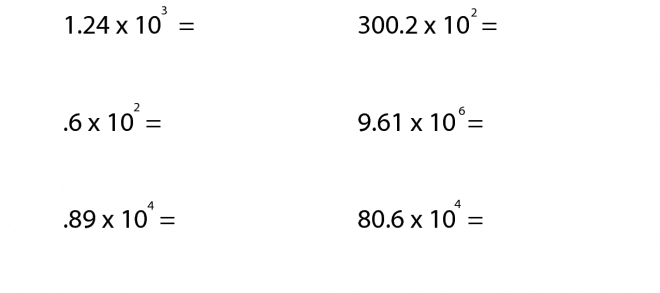5 Ways to Master Long Division of Decimals

Mastering Long Division of Decimals: A Comprehensive Guide
Long division of decimals can be a daunting task for many students, but with practice and the right techniques, it can become a manageable and even straightforward process. In this guide, we will explore five ways to master long division of decimals, from understanding the basics to more advanced techniques.
Understanding the Basics
Before we dive into the five ways to master long division of decimals, let’s first review the basics. Long division of decimals is similar to long division of whole numbers, with a few key differences. When dividing decimals, we need to make sure that we are dividing both the dividend and the divisor by the same power of 10. This ensures that the result is accurate and reliable.
📝 Note: It's essential to line up the decimal points in both the dividend and the divisor, as this will help you keep track of the place values.
Way 1: Using a Calculator
One of the easiest ways to master long division of decimals is to use a calculator. Most calculators have a built-in long division function that can handle decimals with ease. To use a calculator for long division of decimals, simply enter the dividend and the divisor, and the calculator will take care of the rest.
However, while calculators can be a convenient tool, they may not always be available or allowed in certain situations. That’s why it’s essential to learn how to perform long division of decimals manually.
Way 2: Using a Decimal Division Chart
A decimal division chart can be a helpful tool for mastering long division of decimals. A decimal division chart is a table that shows the relationship between the dividend, divisor, quotient, and remainder. By using a decimal division chart, you can quickly and easily find the quotient and remainder of a decimal division problem.
Here’s an example of a decimal division chart:
| Dividend | Divisor | Quotient | Remainder |
|---|---|---|---|
| 12.5 | 2.5 | 5 | 0 |
| 25.2 | 3.1 | 8.13 | 0.01 |
| 46.8 | 6.2 | 7.55 | 0.3 |
Way 3: Using the Partial Quotients Method
The partial quotients method is a manual technique for performing long division of decimals. This method involves breaking down the division problem into smaller parts, finding the partial quotients, and then combining them to find the final result.
Here’s an example of how to use the partial quotients method:
- Divide 12.5 by 2.5 using the partial quotients method:
- Divide 12 by 2.5 = 4
- Multiply 4 by 2.5 = 10
- Subtract 10 from 12.5 = 2.5
- Divide 2.5 by 2.5 = 1
- Add 4 and 1 = 5
Therefore, 12.5 divided by 2.5 is equal to 5.
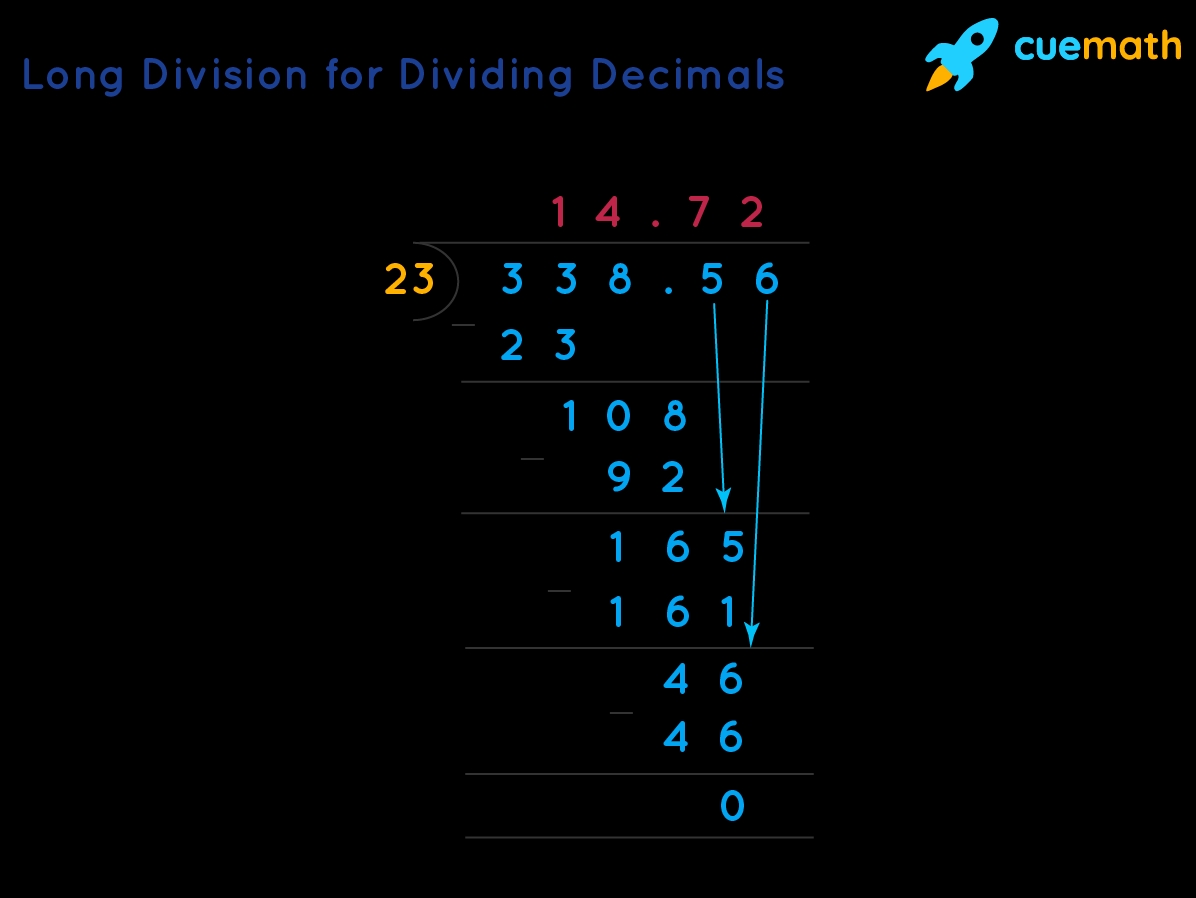
Way 4: Using the Standard Algorithm
The standard algorithm for long division of decimals is a step-by-step process that involves dividing the dividend by the divisor, finding the remainder, and then repeating the process until the remainder is 0.
Here’s an example of how to use the standard algorithm:
- Divide 25.2 by 3.1 using the standard algorithm:
- Divide 25 by 3.1 = 8
- Multiply 8 by 3.1 = 24.8
- Subtract 24.8 from 25.2 = 0.4
- Divide 0.4 by 3.1 = 0.13
- Add 8 and 0.13 = 8.13
Therefore, 25.2 divided by 3.1 is equal to 8.13.
Way 5: Practicing with Real-World Examples
The best way to master long division of decimals is to practice with real-world examples. By using everyday situations, such as measuring ingredients for a recipe or calculating the cost of groceries, you can make long division of decimals more meaningful and relevant.
Here are a few examples of real-world problems that involve long division of decimals:
- A recipe calls for 2.5 cups of flour, but you only have a 1.25 cup measuring cup. How many times will you need to fill the measuring cup to get the right amount of flour?
- A store is having a sale on a certain type of coffee, and a 12-ounce bag is on sale for $2.50. If you want to buy 3 bags, how much will you need to pay in total?
By practicing with real-world examples, you can develop your skills and build your confidence in performing long division of decimals.
Long division of decimals may seem daunting at first, but with practice and the right techniques, it can become a manageable and even straightforward process. By using a calculator, a decimal division chart, the partial quotients method, the standard algorithm, and practicing with real-world examples, you can master long division of decimals and become more confident in your math skills.
Remember, the key to mastering long division of decimals is to practice regularly and to use a variety of techniques to help you understand the process. With time and practice, you’ll become proficient in long division of decimals and be able to tackle even the most challenging problems with ease.
What is the difference between long division of whole numbers and long division of decimals?
+The main difference between long division of whole numbers and long division of decimals is that when dividing decimals, we need to make sure that we are dividing both the dividend and the divisor by the same power of 10.
Can I use a calculator to perform long division of decimals?
+Yes, you can use a calculator to perform long division of decimals. However, it’s also important to learn how to perform long division manually, as calculators may not always be available or allowed in certain situations.
What is the partial quotients method, and how do I use it?
+The partial quotients method is a manual technique for performing long division of decimals. It involves breaking down the division problem into smaller parts, finding the partial quotients, and then combining them to find the final result.
How can I practice long division of decimals in real-world situations?
+You can practice long division of decimals in real-world situations by using everyday examples, such as measuring ingredients for a recipe or calculating the cost of groceries.