5 Ways to Master Inscribed Angles
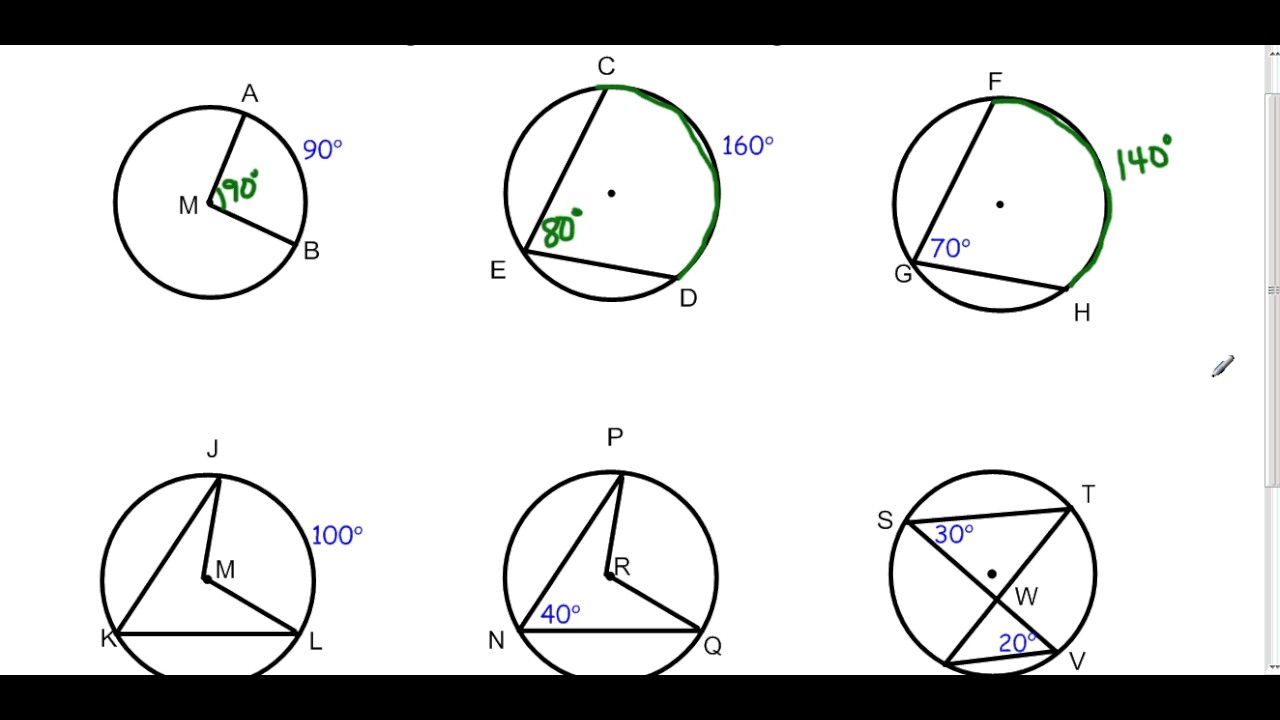
Unlocking the Secrets of Inscribed Angles
Inscribed angles are a fundamental concept in geometry, and mastering them can make a significant difference in your problem-solving skills. Whether you’re a student or a teacher, understanding inscribed angles can help you tackle complex problems with ease. In this article, we’ll explore five ways to master inscribed angles and take your geometry skills to the next level.
What are Inscribed Angles?
Before we dive into the techniques, let’s define what inscribed angles are. An inscribed angle is an angle whose vertex is on a circle and whose sides contain chords of the circle. The angle is said to be inscribed in the circle. Inscribed angles have some unique properties that make them useful in solving problems.
1. Understanding the Inscribed Angle Theorem
The Inscribed Angle Theorem states that the measure of an inscribed angle is equal to half the measure of its intercepted arc. This theorem is the foundation of inscribed angles, and understanding it is crucial to mastering the concept. Here’s how to apply the theorem:
- Identify the inscribed angle and its intercepted arc.
- Measure the intercepted arc.
- Divide the measure of the arc by 2 to find the measure of the inscribed angle.
📝 Note: The Inscribed Angle Theorem only applies to inscribed angles, not central angles or other types of angles.
2. Mastering the Properties of Inscribed Angles
Inscribed angles have some unique properties that can help you solve problems. Here are some key properties to remember:
- Inscribed angles are congruent if their intercepted arcs are congruent. This means that if two inscribed angles intercept the same arc, they are congruent.
- Inscribed angles are supplementary if their intercepted arcs are adjacent. This means that if two inscribed angles intercept adjacent arcs, they are supplementary.
- The measure of an inscribed angle is half the measure of its intercepted arc. This is a direct application of the Inscribed Angle Theorem.
By mastering these properties, you can solve problems involving inscribed angles with ease.
3. Solving Problems with Inscribed Angles
Now that you understand the Inscribed Angle Theorem and the properties of inscribed angles, it’s time to practice solving problems. Here are some examples:
- Find the measure of an inscribed angle if the intercepted arc measures 120°.
- Find the measure of an inscribed angle if it is supplementary to another angle that intercepts an arc of 60°.
- Find the measure of an inscribed angle if it intercepts an arc that is congruent to another arc intercepted by a 30° angle.
By practicing these types of problems, you’ll become more comfortable working with inscribed angles.
4. Applying Inscribed Angles to Real-World Problems
Inscribed angles have many real-world applications, from architecture to engineering. Here are some examples:
- Designing a bridge: Inscribed angles can be used to determine the angle of a bridge’s arch.
- Building a dome: Inscribed angles can be used to determine the angle of a dome’s curve.
- Designing a roller coaster: Inscribed angles can be used to determine the angle of a roller coaster’s curve.
By applying inscribed angles to real-world problems, you can see the practical value of mastering this concept.
5. Using Technology to Visualize Inscribed Angles
Technology can be a powerful tool for visualizing inscribed angles. Here are some ways to use technology to master inscribed angles:
- Geometry software: Use software like GeoGebra or SketchUp to create interactive models of inscribed angles.
- Online calculators: Use online calculators to practice solving problems involving inscribed angles.
- Interactive simulations: Use interactive simulations to explore the properties of inscribed angles.
By using technology to visualize inscribed angles, you can gain a deeper understanding of the concept and improve your problem-solving skills.
In summary, mastering inscribed angles requires a combination of theoretical knowledge, problem-solving skills, and practical application. By understanding the Inscribed Angle Theorem, mastering the properties of inscribed angles, solving problems, applying inscribed angles to real-world problems, and using technology to visualize inscribed angles, you can become proficient in working with inscribed angles.
The key takeaways from this article are:
- The Inscribed Angle Theorem states that the measure of an inscribed angle is equal to half the measure of its intercepted arc.
- Inscribed angles have unique properties, such as being congruent if their intercepted arcs are congruent.
- Inscribed angles can be applied to real-world problems, such as designing a bridge or building a dome.
- Technology can be used to visualize inscribed angles and improve problem-solving skills.
By mastering inscribed angles, you can improve your geometry skills and tackle complex problems with ease.
What is the Inscribed Angle Theorem?
+The Inscribed Angle Theorem states that the measure of an inscribed angle is equal to half the measure of its intercepted arc.
What are some properties of inscribed angles?
+Inscribed angles are congruent if their intercepted arcs are congruent, supplementary if their intercepted arcs are adjacent, and have a measure equal to half the measure of their intercepted arc.
How can I apply inscribed angles to real-world problems?
+Inscribed angles can be applied to real-world problems such as designing a bridge, building a dome, or designing a roller coaster.
Related Terms:
- Inscribed Angles Worksheet PDF
- Inscribed Angles Worksheet answers
- Inscribed and central angles worksheet
- Kuta Software Inscribed Angles
- Homework 5 Inscribed Angles worksheet