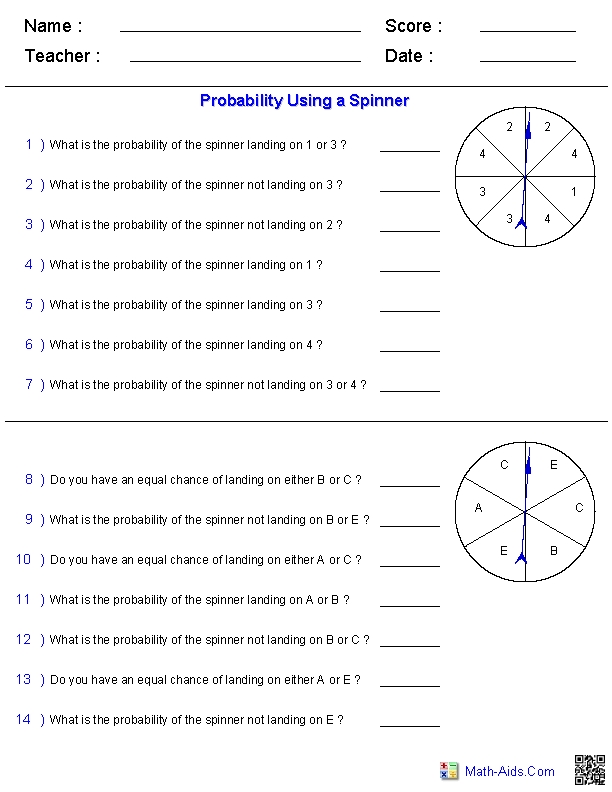
Probability Worksheets With Answers
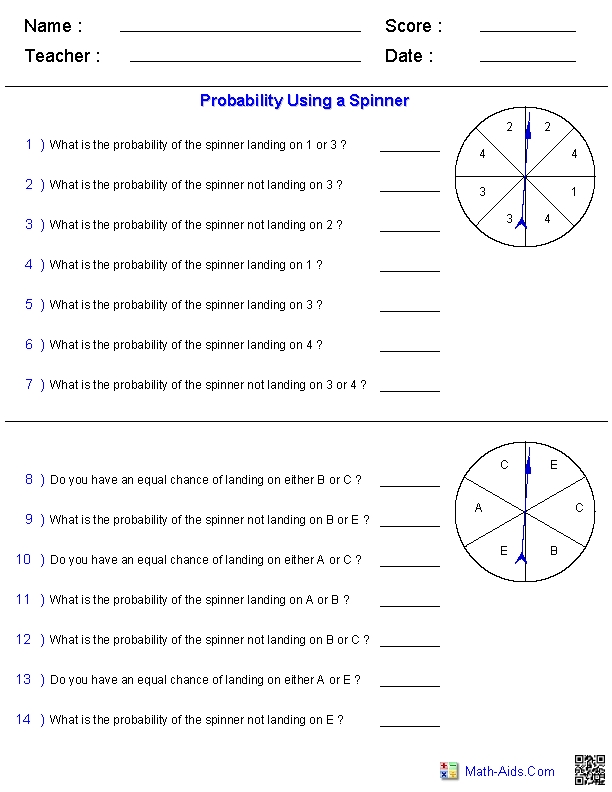
Mastering Probability: A Comprehensive Guide with Worksheets and Answers
Probability is a fundamental concept in mathematics that deals with the chance or likelihood of an event occurring. It is a crucial aspect of statistics, data analysis, and decision-making. In this article, we will provide a comprehensive guide to probability, including worksheets with answers, to help students and learners master this essential concept.
What is Probability?
Probability is a measure of the likelihood of an event occurring. It is expressed as a numerical value between 0 and 1, where 0 indicates an impossible event and 1 indicates a certain event. The probability of an event is calculated by dividing the number of favorable outcomes by the total number of possible outcomes.
Types of Probability
There are two main types of probability:
- Theoretical Probability: This type of probability is based on the number of favorable outcomes and the total number of possible outcomes. It is calculated using the formula: P(event) = Number of favorable outcomes / Total number of possible outcomes.
- Experimental Probability: This type of probability is based on the results of repeated trials or experiments. It is calculated by dividing the number of times the event occurs by the total number of trials.
Probability Worksheets with Answers
Here are five probability worksheets with answers to help you practice and master the concept:
Worksheet 1: Basic Probability
| Event | Number of Favorable Outcomes | Total Number of Possible Outcomes | Probability |
|---|---|---|---|
| Rolling a 6 on a fair die | 1 | 6 | ? |
| Drawing an ace from a deck of cards | 4 | 52 | ? |
| Flipping a head on a fair coin | 1 | 2 | ? |
Answers:
- Rolling a 6 on a fair die: P(event) = 1⁄6 = 0.17
- Drawing an ace from a deck of cards: P(event) = 4⁄52 = 0.08
- Flipping a head on a fair coin: P(event) = 1⁄2 = 0.5
Worksheet 2: Probability of Independent Events
| Event | Probability |
|---|---|
| Rolling a 6 on a fair die | 1⁄6 |
| Drawing an ace from a deck of cards | 4⁄52 |
| Flipping a head on a fair coin | 1⁄2 |
| Probability of rolling a 6 and drawing an ace | ? |
| Probability of flipping a head and drawing an ace | ? |
Answers:
- Probability of rolling a 6 and drawing an ace: P(event) = (1⁄6) × (4⁄52) = 1⁄78
- Probability of flipping a head and drawing an ace: P(event) = (1⁄2) × (4⁄52) = 1⁄26
Worksheet 3: Probability of Dependent Events
| Event | Probability |
|---|---|
| Drawing an ace from a deck of cards | 4⁄52 |
| Drawing a king from the same deck | 4⁄51 |
| Probability of drawing an ace and then a king | ? |
| Probability of drawing a king and then an ace | ? |
Answers:
- Probability of drawing an ace and then a king: P(event) = (4⁄52) × (4⁄51) = 4⁄663
- Probability of drawing a king and then an ace: P(event) = (4⁄51) × (3⁄51) = 12⁄2601
Worksheet 4: Probability of Mutually Exclusive Events
| Event | Probability |
|---|---|
| Rolling a 6 on a fair die | 1⁄6 |
| Rolling a 5 on a fair die | 1⁄6 |
| Probability of rolling a 6 or a 5 | ? |
| Probability of rolling a 6 or a 3 | ? |
Answers:
- Probability of rolling a 6 or a 5: P(event) = (1⁄6) + (1⁄6) = 1⁄3
- Probability of rolling a 6 or a 3: P(event) = (1⁄6) + (1⁄6) = 1⁄3
Worksheet 5: Real-World Applications of Probability
| Event | Probability |
|---|---|
| It will rain tomorrow | 0.7 |
| It will not rain tomorrow | 0.3 |
| Probability of it raining tomorrow and the next day | ? |
| Probability of it not raining tomorrow and the next day | ? |
Answers:
- Probability of it raining tomorrow and the next day: P(event) = (0.7) × (0.7) = 0.49
- Probability of it not raining tomorrow and the next day: P(event) = (0.3) × (0.3) = 0.09
📝 Note: These worksheets are meant to provide a comprehensive guide to probability and are not exhaustive. Practice with different types of problems to master the concept.
Conclusion
Probability is a fundamental concept in mathematics that has numerous real-world applications. Mastering probability requires a deep understanding of the different types of probability, including theoretical and experimental probability. The worksheets provided in this article are designed to help students and learners practice and master the concept of probability. By practicing with different types of problems, you can develop a strong foundation in probability and apply it to various real-world scenarios.
What is the difference between theoretical and experimental probability?
+Theoretical probability is based on the number of favorable outcomes and the total number of possible outcomes, while experimental probability is based on the results of repeated trials or experiments.
How do I calculate the probability of independent events?
+To calculate the probability of independent events, multiply the probabilities of each event together.
What are mutually exclusive events?
+Mutually exclusive events are events that cannot occur together. For example, rolling a 6 and rolling a 5 on a fair die are mutually exclusive events.