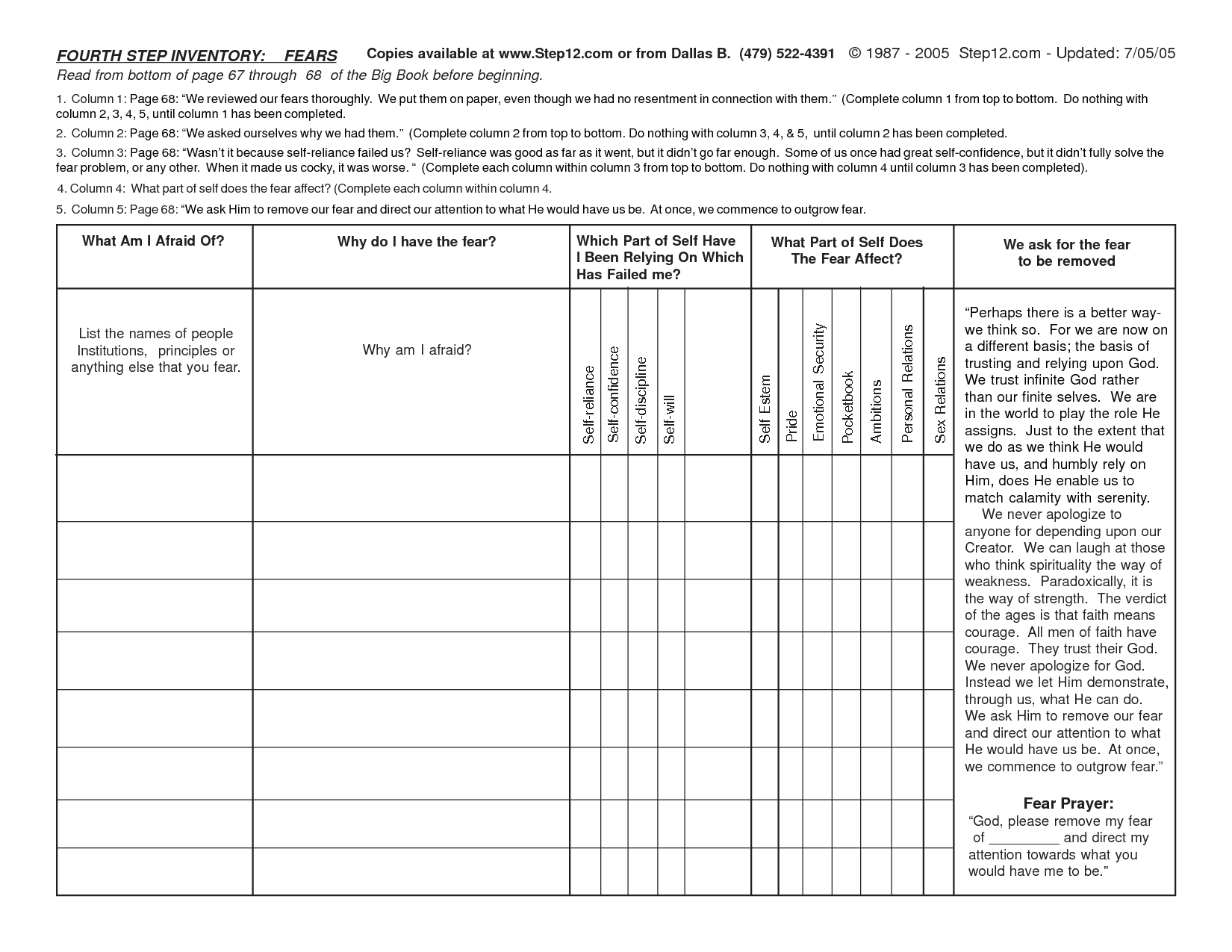
Systems Of Linear Inequalities Worksheet

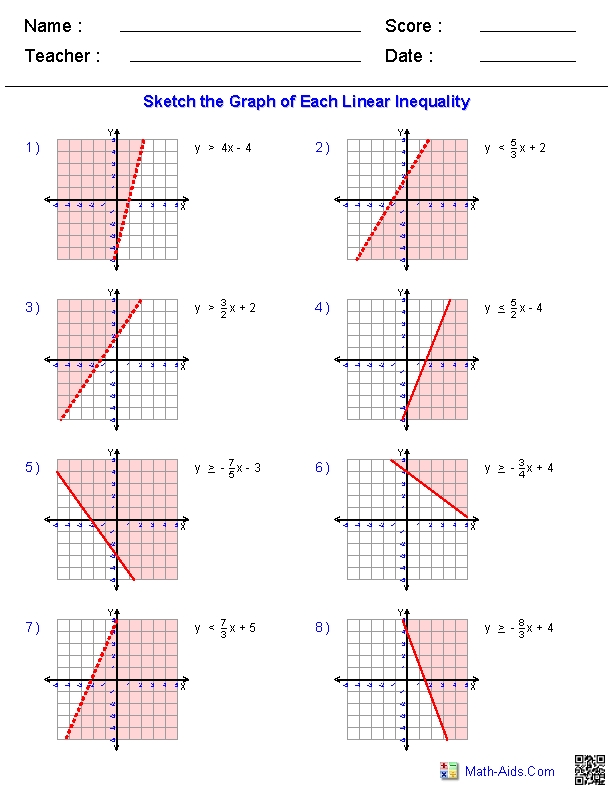
Systems of Linear Inequalities Worksheet

Solving systems of linear inequalities is a fundamental concept in algebra and mathematics. This worksheet is designed to help students practice and master this concept. Below, we’ll explore what systems of linear inequalities are, how to solve them, and provide a comprehensive worksheet with exercises.

What are Systems of Linear Inequalities?

A system of linear inequalities consists of two or more linear inequalities that share common variables. These inequalities can be in the form of “less than,” “greater than,” “less than or equal to,” or “greater than or equal to.” The goal is to find the solution set that satisfies all the inequalities simultaneously.

How to Solve Systems of Linear Inequalities

Solving systems of linear inequalities involves several steps:

1. Graph the first inequality: Plot the boundary line and shade the region that satisfies the inequality.
2. Graph the second inequality: Plot the boundary line and shade the region that satisfies the inequality.
3. Find the intersection: Identify the region where both inequalities are satisfied.

Step-by-Step Solution

Let’s consider an example:

Solve the system of linear inequalities:

2x + 3y ≤ 12

x - 2y ≥ -3

Step 1: Graph the first inequality

The boundary line is 2x + 3y = 12.

To graph this line, we can use two points. Let’s choose (0, 4) and (6, 0).

Now, we need to shade the region that satisfies the inequality. Since the inequality is “less than or equal to,” we shade the region below the line.

Step 2: Graph the second inequality

The boundary line is x - 2y = -3.

To graph this line, we can use two points. Let’s choose (0, -1.5) and (3, 0).

Now, we need to shade the region that satisfies the inequality. Since the inequality is “greater than or equal to,” we shade the region above the line.

Step 3: Find the intersection

The region where both inequalities are satisfied is the shaded area.

Notes

• When graphing the second inequality, we need to be careful not to erase the first inequality.
• The solution set is the region where both inequalities are satisfied.

Systems of Linear Inequalities Worksheet

Now, it’s time to practice! Below are some exercises to help you master systems of linear inequalities.

Exercise 1

Solve the system of linear inequalities:

x + 2y ≤ 8

3x - 2y ≥ -4

Exercise 2

Solve the system of linear inequalities:

2x - 3y ≤ 9

x + 4y ≥ 8

Exercise 3

Solve the system of linear inequalities:

x - 2y ≤ 5

3x + 2y ≥ 6

Exercise 4

Solve the system of linear inequalities:

2x + 5y ≤ 15

x - 3y ≥ -2

Exercise 5

Solve the system of linear inequalities:

x + 3y ≤ 12

2x - 2y ≥ -4

Exercise 6

Solve the system of linear inequalities:

3x - 4y ≤ 8

2x + 3y ≥ 5

Exercise 7

Solve the system of linear inequalities:

x - 3y ≤ 6

2x + 2y ≥ 4

Exercise 8

Solve the system of linear inequalities:

2x - 5y ≤ 10

x + 4y ≥ 8

Exercise 9

Solve the system of linear inequalities:

x + 2y ≤ 9

3x - 3y ≥ -3

Exercise 10

Solve the system of linear inequalities:

2x - 2y ≤ 6

x + 3y ≥ 5

To solve these exercises, follow the steps outlined above.

Summary

In this worksheet, we’ve explored systems of linear inequalities and provided exercises to help you practice. Remember to graph the inequalities carefully and find the intersection of the shaded regions.