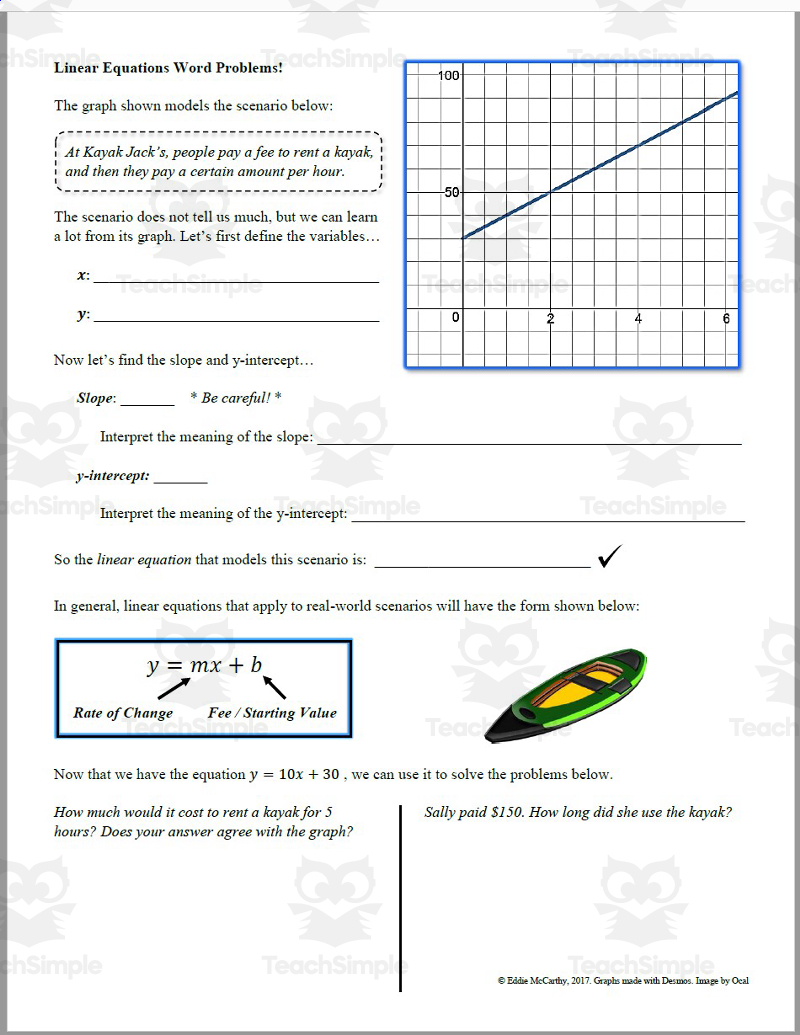
Convert 7 Improper Fractions to Mixed Numbers Easily
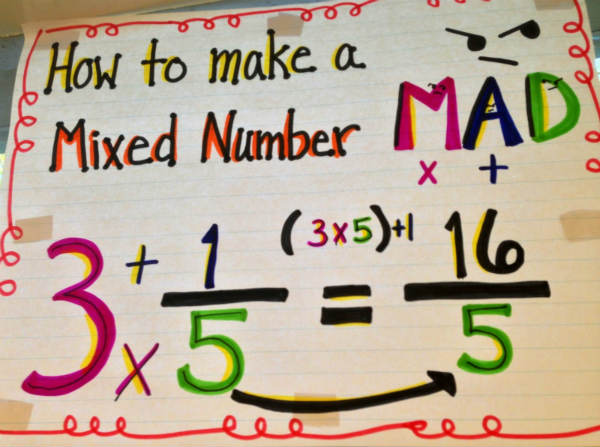
Understanding Improper Fractions and Mixed Numbers
Improper fractions and mixed numbers are two different ways to represent the same value in mathematics. An improper fraction is a fraction where the numerator (the top number) is greater than the denominator (the bottom number). On the other hand, a mixed number is a combination of a whole number and a proper fraction.
For example, the improper fraction 3⁄2 can be converted to the mixed number 1 1⁄2.
Why Convert Improper Fractions to Mixed Numbers?
Converting improper fractions to mixed numbers can be helpful in various situations, such as:
- Simplifying calculations: Mixed numbers can make calculations easier, especially when dealing with fractions in real-world applications.
- Improving readability: Mixed numbers can be easier to read and understand, especially for fractions with large numerators.
- Enhancing visualization: Mixed numbers can help visualize the value of a fraction more easily, making it more intuitive to work with.
Step-by-Step Guide to Converting Improper Fractions to Mixed Numbers
Converting an improper fraction to a mixed number is a simple process. Here’s a step-by-step guide:
- Divide the numerator by the denominator: Divide the top number (numerator) by the bottom number (denominator).
- Find the quotient and remainder: The result of the division will give you a quotient (whole number part) and a remainder (fraction part).
- Write the mixed number: Write the quotient as the whole number part, and the remainder as the fraction part.
Let’s illustrate this with an example:
Suppose we want to convert the improper fraction 7⁄4 to a mixed number.
- Divide the numerator by the denominator: 7 ÷ 4 = 1 with a remainder of 3.
- Find the quotient and remainder: The quotient is 1, and the remainder is 3.
- Write the mixed number: The mixed number is 1 3⁄4.
Converting 7 Improper Fractions to Mixed Numbers
Here are 7 examples of improper fractions converted to mixed numbers:
- Improper fraction: 9⁄2
- Divide the numerator by the denominator: 9 ÷ 2 = 4 with a remainder of 1.
- Write the mixed number: 4 1⁄2
- Improper fraction: 11⁄3
- Divide the numerator by the denominator: 11 ÷ 3 = 3 with a remainder of 2.
- Write the mixed number: 3 2⁄3
- Improper fraction: 13⁄4
- Divide the numerator by the denominator: 13 ÷ 4 = 3 with a remainder of 1.
- Write the mixed number: 3 1⁄4
- Improper fraction: 15⁄5
- Divide the numerator by the denominator: 15 ÷ 5 = 3 with a remainder of 0.
- Write the mixed number: 3 0/5 (or simply 3)
- Improper fraction: 17⁄6
- Divide the numerator by the denominator: 17 ÷ 6 = 2 with a remainder of 5.
- Write the mixed number: 2 5⁄6
- Improper fraction: 19⁄8
- Divide the numerator by the denominator: 19 ÷ 8 = 2 with a remainder of 3.
- Write the mixed number: 2 3⁄8
- Improper fraction: 21⁄9
- Divide the numerator by the denominator: 21 ÷ 9 = 2 with a remainder of 3.
- Write the mixed number: 2 3⁄9
p class=“pro-note”> 🤔 Note:
When converting improper fractions to mixed numbers, make sure to simplify the fraction part, if possible. For example, 2 4⁄8 can be simplified to 2 1⁄2.
By following these simple steps, you can easily convert improper fractions to mixed numbers.
Related Terms:
- Adding mixed numbers Worksheet