6 Ways to Master Adding Fractions With Like Denominators

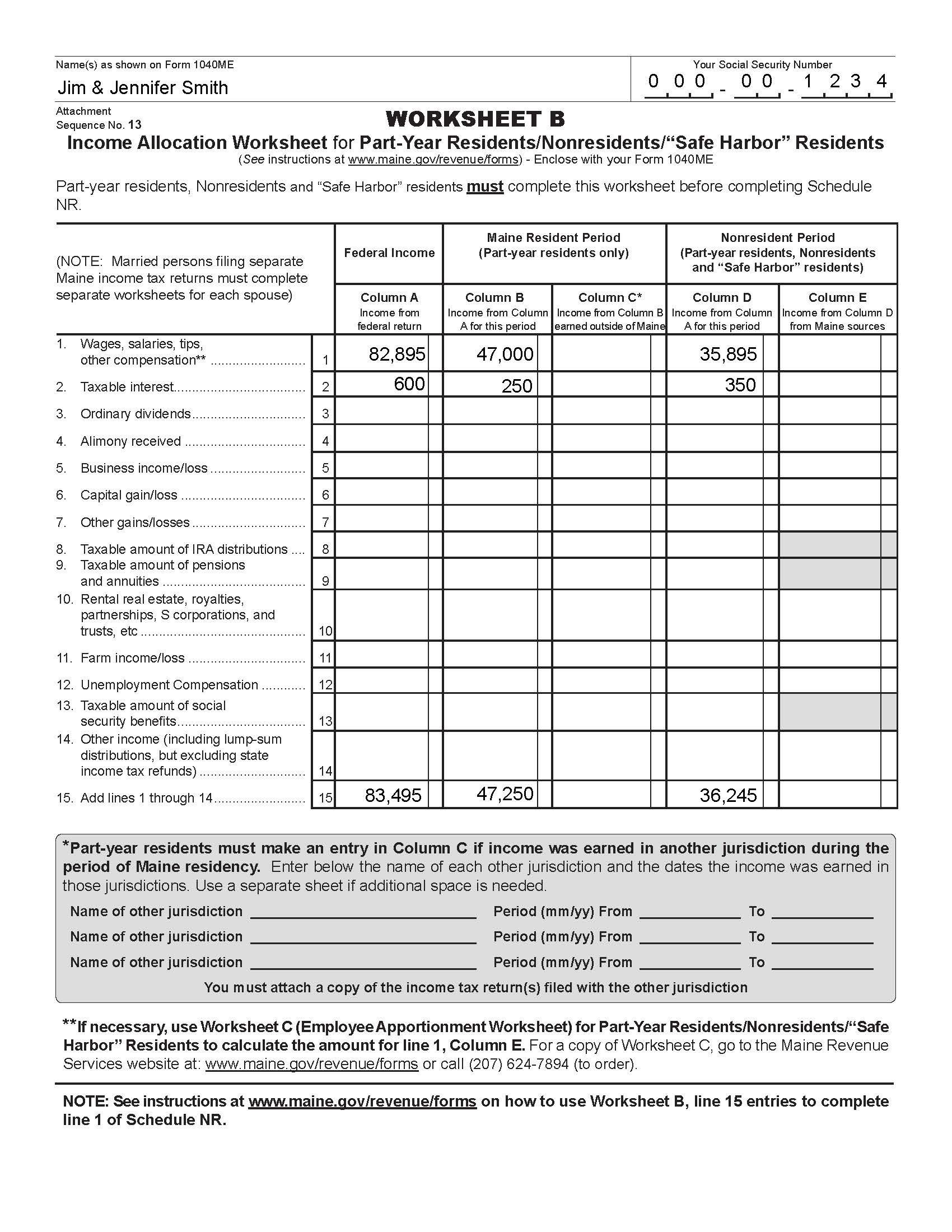
Understanding Fractions and Like Denominators
Fractions are a fundamental concept in mathematics, and adding fractions with like denominators is a crucial skill to master. In this blog post, we will explore six ways to help you master adding fractions with like denominators. Before we dive into the methods, let’s first understand what fractions and like denominators are.
A fraction is a way to represent a part of a whole. It consists of two parts: the numerator and the denominator. The numerator represents the number of equal parts, while the denominator represents the total number of parts.
Like denominators refer to fractions that have the same denominator. For example, 1⁄4 and 3⁄4 are like denominators because they both have a denominator of 4.
Method 1: Visualizing Fractions
One way to master adding fractions with like denominators is to visualize them. You can use real-life objects or drawings to represent the fractions. For example, let’s say you want to add 1⁄4 and 3⁄4. You can draw a pizza that is divided into 4 equal parts. Shade 1 part for the first fraction and 3 parts for the second fraction. Then, count the total number of shaded parts to get the answer.
Example:
1⁄4 + 3⁄4 =?
Draw a pizza with 4 equal parts. Shade 1 part for the first fraction and 3 parts for the second fraction.
Total shaded parts = 4
Answer: 4⁄4 = 1
🤔 Note: Visualizing fractions can help you understand the concept better, but it may not be practical for larger numbers.
Method 2: Using Number Lines
Another way to add fractions with like denominators is to use number lines. A number line is a visual representation of numbers on a line. You can use a number line to show the relationship between fractions with like denominators.
For example, let’s say you want to add 1⁄4 and 3⁄4. You can draw a number line with marks at 0, 1⁄4, 2⁄4, 3⁄4, and 4⁄4. Then, count the number of units between 1⁄4 and 3⁄4 to get the answer.
Example:
1⁄4 + 3⁄4 =?
Draw a number line with marks at 0, 1⁄4, 2⁄4, 3⁄4, and 4⁄4.
Count the number of units between 1⁄4 and 3⁄4 = 2 units
Answer: 2⁄4 = 1⁄2
Method 3: Using Fraction Strips
Fraction strips are a hands-on way to add fractions with like denominators. You can use paper strips or blocks to represent the fractions. For example, let’s say you want to add 1⁄4 and 3⁄4. You can use 4 strips to represent the denominator and shade 1 strip for the first fraction and 3 strips for the second fraction. Then, count the total number of shaded strips to get the answer.
Example:
1⁄4 + 3⁄4 =?
Use 4 strips to represent the denominator. Shade 1 strip for the first fraction and 3 strips for the second fraction.
Total shaded strips = 4
Answer: 4⁄4 = 1
👍 Note: Fraction strips can be a fun and interactive way to learn about fractions, but they may not be suitable for larger numbers.
Method 4: Using the Standard Algorithm
The standard algorithm is a step-by-step method for adding fractions with like denominators. To use the standard algorithm, follow these steps:
- Write the fractions with like denominators.
- Add the numerators.
- Keep the denominator the same.
- Simplify the answer, if possible.
Example:
1⁄4 + 3⁄4 =?
Add the numerators: 1 + 3 = 4
Keep the denominator the same: 4
Answer: 4⁄4 = 1
Method 5: Using Real-World Applications
Adding fractions with like denominators can be used in real-world applications, such as cooking, building, and finance. For example, let’s say you want to add 1⁄4 cup of sugar and 3⁄4 cup of sugar to a recipe. You can use the standard algorithm to add the fractions.
Example:
1⁄4 cup + 3⁄4 cup =?
Add the numerators: 1 + 3 = 4
Keep the denominator the same: 4
Answer: 4⁄4 cup = 1 cup
Method 6: Practicing with Online Resources
There are many online resources available to help you practice adding fractions with like denominators. You can use websites, apps, and games to practice adding fractions in a fun and interactive way.
Some popular online resources include:
- Khan Academy
- Mathway
- IXL
- Coolmath
📊 Note: Practicing with online resources can help you build your confidence and fluency in adding fractions with like denominators.
Mastering adding fractions with like denominators takes practice and patience. By using these six methods, you can build your skills and become proficient in adding fractions with like denominators.
In conclusion, adding fractions with like denominators is an essential skill in mathematics. By visualizing fractions, using number lines, fraction strips, the standard algorithm, real-world applications, and practicing with online resources, you can master adding fractions with like denominators.
What are like denominators?
+Like denominators refer to fractions that have the same denominator.
How do I add fractions with like denominators?
+To add fractions with like denominators, follow these steps: write the fractions with like denominators, add the numerators, keep the denominator the same, and simplify the answer, if possible.
What are some real-world applications of adding fractions with like denominators?
+Adding fractions with like denominators can be used in real-world applications, such as cooking, building, and finance.