Domain and Range Worksheet Solutions Made Easy

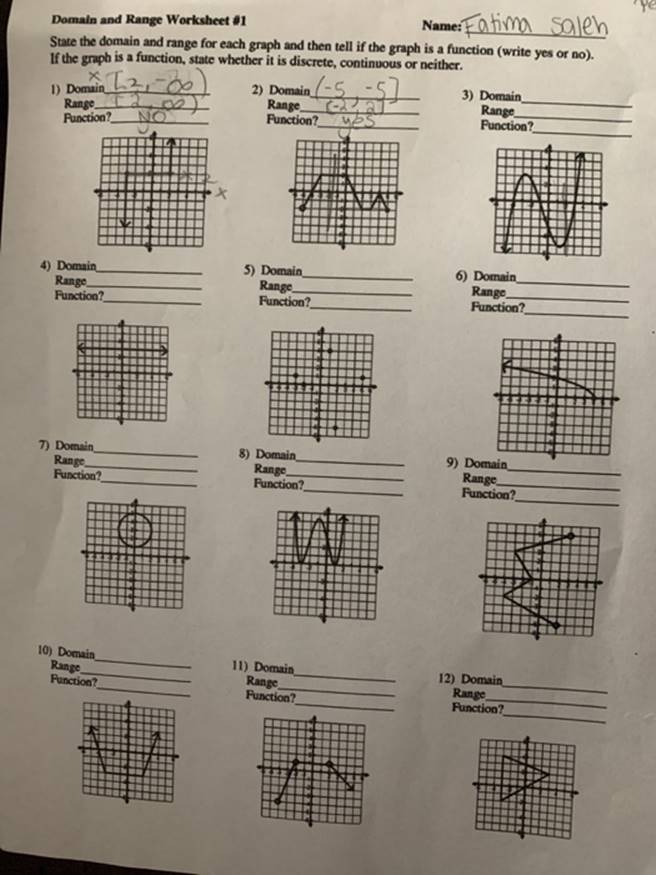
Understanding Domain and Range: A Comprehensive Guide

When dealing with functions in mathematics, two fundamental concepts that play a crucial role in understanding the behavior of these functions are domain and range. The domain of a function is the set of all possible input values for which the function is defined, while the range is the set of all possible output values. In this article, we will delve into the world of domain and range, providing a comprehensive guide to help you grasp these concepts with ease.

What is Domain?

The domain of a function is the set of all possible input values for which the function is defined. In other words, it is the set of all values that can be plugged into the function without resulting in an undefined or imaginary output. The domain is typically represented as a set of values in interval notation, with square brackets denoting closed intervals (including the endpoints) and parentheses denoting open intervals (excluding the endpoints).

How to Find the Domain of a Function

To find the domain of a function, follow these steps:

• Identify the type of function (linear, quadratic, polynomial, rational, etc.)
• Check for any restrictions on the input values, such as division by zero or taking the square root of a negative number
• Consider the graph of the function, if available
• Express the domain in interval notation

What is Range?

The range of a function is the set of all possible output values. It represents the set of values that the function can produce. The range is also represented in interval notation.

How to Find the Range of a Function

To find the range of a function, follow these steps:

• Identify the type of function
• Analyze the behavior of the function as the input values approach positive or negative infinity
• Check for any maximum or minimum values
• Express the range in interval notation

Domain and Range Examples

Let’s consider some examples to illustrate the concepts of domain and range:

Example 1: Domain and Range of a Linear Function

Consider the linear function:

f(x) = 2x + 1

The domain of this function is all real numbers, as there are no restrictions on the input values.

Domain: (-∞, ∞)

Range: (-∞, ∞)

Example 2: Domain and Range of a Quadratic Function

Consider the quadratic function:

f(x) = x^2 + 1

The domain of this function is also all real numbers, as there are no restrictions on the input values.

Domain: (-∞, ∞)

Range: [1, ∞)

Note that the range is restricted to values greater than or equal to 1, as the quadratic function has a minimum value of 1.

Example 3: Domain and Range of a Rational Function

Consider the rational function:

f(x) = 1/x

The domain of this function is restricted to all real numbers except zero, as division by zero is undefined.

Domain: (-∞, 0) ∪ (0, ∞)

Range: (-∞, 0) ∪ (0, ∞)

Note that the range is also restricted to all real numbers except zero, as the function can never produce a value of zero.

Domain and Range Worksheet Solutions

To help you better understand the concepts of domain and range, here are some practice questions with solutions:

Question 1:

Find the domain and range of the function:

f(x) = √(x - 1)

Domain: [1, ∞)

Range: [0, ∞)

Question 2:

Find the domain and range of the function:

f(x) = 1/(x - 2)

Domain: (-∞, 2) ∪ (2, ∞)

Range: (-∞, 0) ∪ (0, ∞)

Question 3:

Find the domain and range of the function:

f(x) = x^3 - 2x^2 + x - 1

Domain: (-∞, ∞)

Range: (-∞, ∞)

📝 Note: These are just a few examples to illustrate the concepts of domain and range. For more practice, try solving additional problems or create your own worksheets.

When it comes to domain and range, it’s essential to understand that each type of function has its unique characteristics. By mastering these concepts, you’ll be able to tackle even the most complex functions with ease.

With practice and patience, you’ll become proficient in finding the domain and range of various functions, from simple linear equations to complex rational expressions.