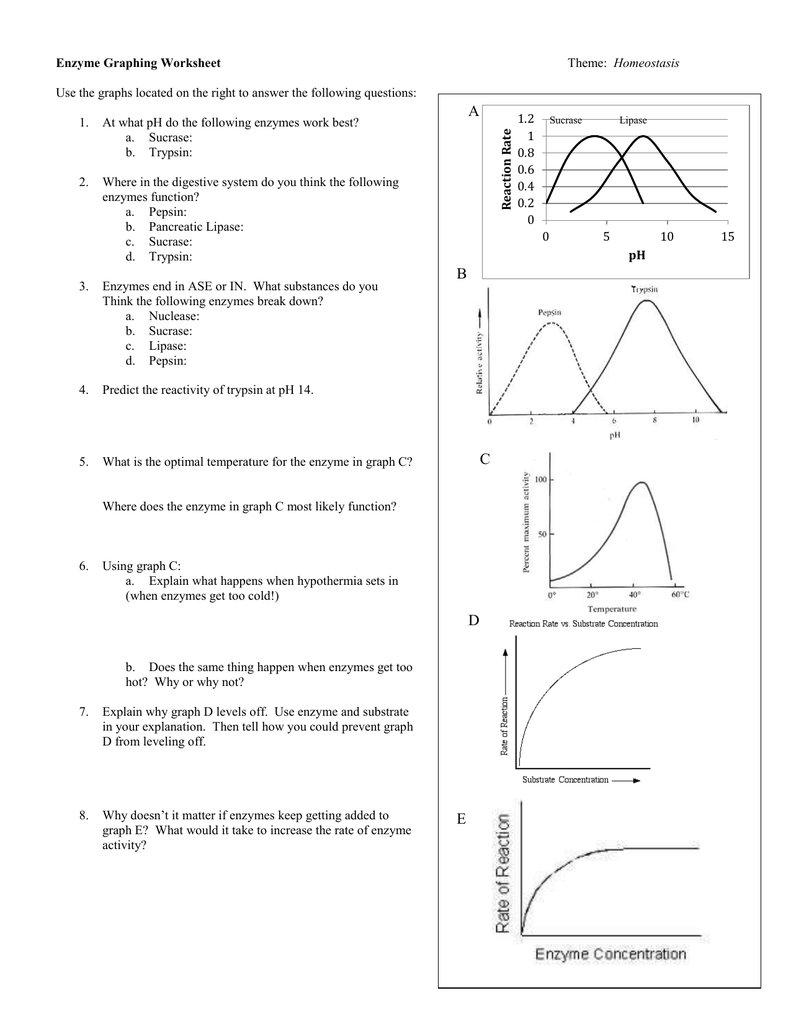
5 Ways to Master Constant of Proportionality Graphs
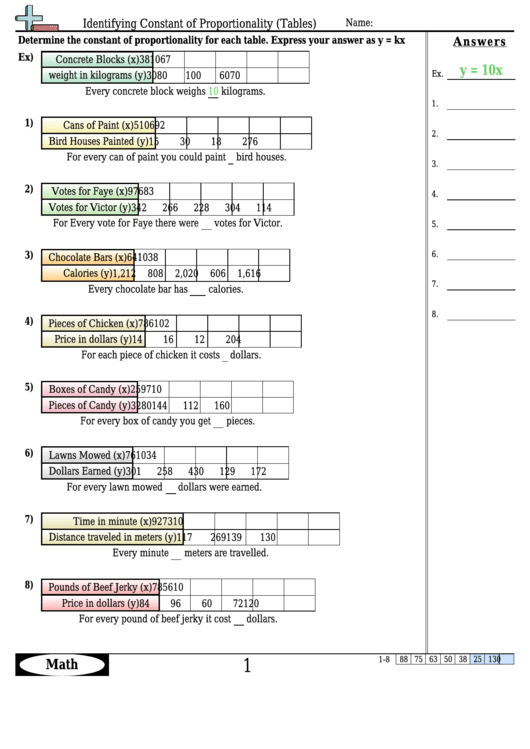
Unlocking the Secrets of Constant of Proportionality Graphs
Constant of proportionality graphs is a fundamental concept in mathematics, particularly in algebra and geometry. It represents the relationship between two quantities that are directly proportional to each other. Mastering constant of proportionality graphs is essential for problem-solving and critical thinking in various fields, including science, engineering, and economics. In this article, we will explore five ways to master constant of proportionality graphs, providing you with a comprehensive understanding of this crucial concept.
Understanding the Basics
Before diving into the strategies, it’s essential to understand the basics of constant of proportionality graphs. A constant of proportionality graph represents the relationship between two quantities, x and y, that are directly proportional to each other. The graph is a straight line that passes through the origin (0, 0), and the slope of the line represents the constant of proportionality.
📝 Note: The constant of proportionality is often represented by the letter 'k'.
Strategy 1: Identifying the Constant of Proportionality
To master constant of proportionality graphs, you need to be able to identify the constant of proportionality from a given graph or table of values. To do this, follow these steps:
- Look for the point on the graph where x = 1.
- Read the corresponding y-value from the graph.
- The y-value represents the constant of proportionality (k).
For example, if the point (1, 3) is on the graph, then the constant of proportionality is 3.
Strategy 2: Using the Constant of Proportionality to Find Missing Values
Once you have identified the constant of proportionality, you can use it to find missing values in a table or graph. To do this, follow these steps:
- Write the equation of the line in the form y = kx.
- Plug in the known values of x and y to find the missing value.
For example, if the constant of proportionality is 2 and you want to find the value of y when x = 4, you can use the equation y = 2x to find y = 8.
Strategy 3: Graphing Constant of Proportionality Graphs
Graphing constant of proportionality graphs is an essential skill for visualizing the relationship between two quantities. To graph a constant of proportionality graph, follow these steps:
- Identify the constant of proportionality (k).
- Write the equation of the line in the form y = kx.
- Plot two points on the graph, such as (0, 0) and (1, k).
- Draw a straight line through the two points.
For example, if the constant of proportionality is 3, the equation of the line would be y = 3x. You can plot the points (0, 0) and (1, 3) and draw a straight line through them.
Strategy 4: Solving Word Problems Involving Constant of Proportionality
Constant of proportionality graphs can be used to solve word problems involving direct proportions. To solve these problems, follow these steps:
- Read the problem carefully and identify the variables and constants.
- Write an equation representing the relationship between the variables.
- Use the equation to find the solution to the problem.
For example, if a bakery sells 250 loaves of bread at $2 each, how much will they sell 500 loaves for? If we assume that the price per loaf is constant, we can use the equation y = 2x to find the solution.
Strategy 5: Applying Constant of Proportionality Graphs to Real-World Situations
Constant of proportionality graphs can be applied to various real-world situations, such as physics, engineering, and economics. To apply constant of proportionality graphs to real-world situations, follow these steps:
- Identify the variables and constants in the situation.
- Write an equation representing the relationship between the variables.
- Use the equation to make predictions or solve problems.
For example, if a car travels 250 miles in 5 hours, how far will it travel in 10 hours? If we assume that the speed of the car is constant, we can use the equation y = 50x to find the solution.
Mastering constant of proportionality graphs takes practice and patience. By following these five strategies, you can develop a deep understanding of this fundamental concept and apply it to various real-world situations.
What is the constant of proportionality?
+
The constant of proportionality is the ratio of the y-value to the x-value in a direct proportionality relationship. It is often represented by the letter ‘k’.
How do I graph a constant of proportionality graph?
+
To graph a constant of proportionality graph, identify the constant of proportionality (k), write the equation of the line in the form y = kx, plot two points on the graph, such as (0, 0) and (1, k), and draw a straight line through the two points.
What are some real-world applications of constant of proportionality graphs?
+
Constant of proportionality graphs can be applied to various real-world situations, such as physics, engineering, and economics, to make predictions or solve problems.