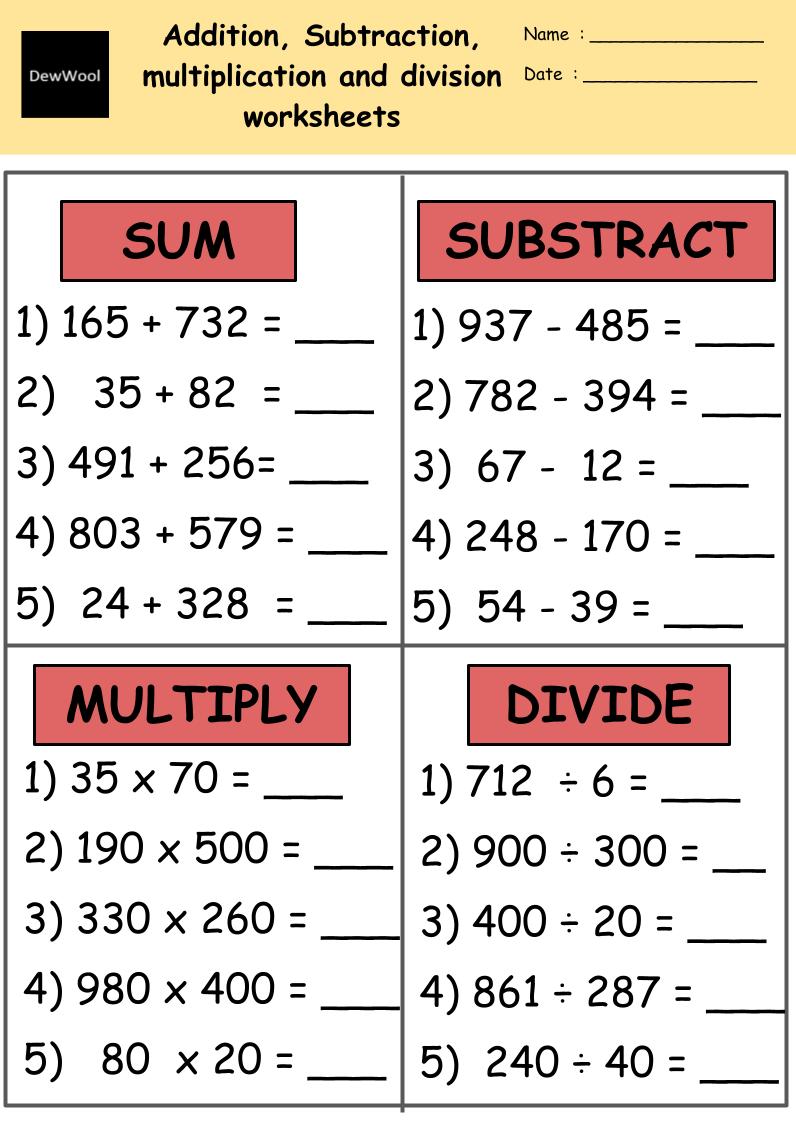
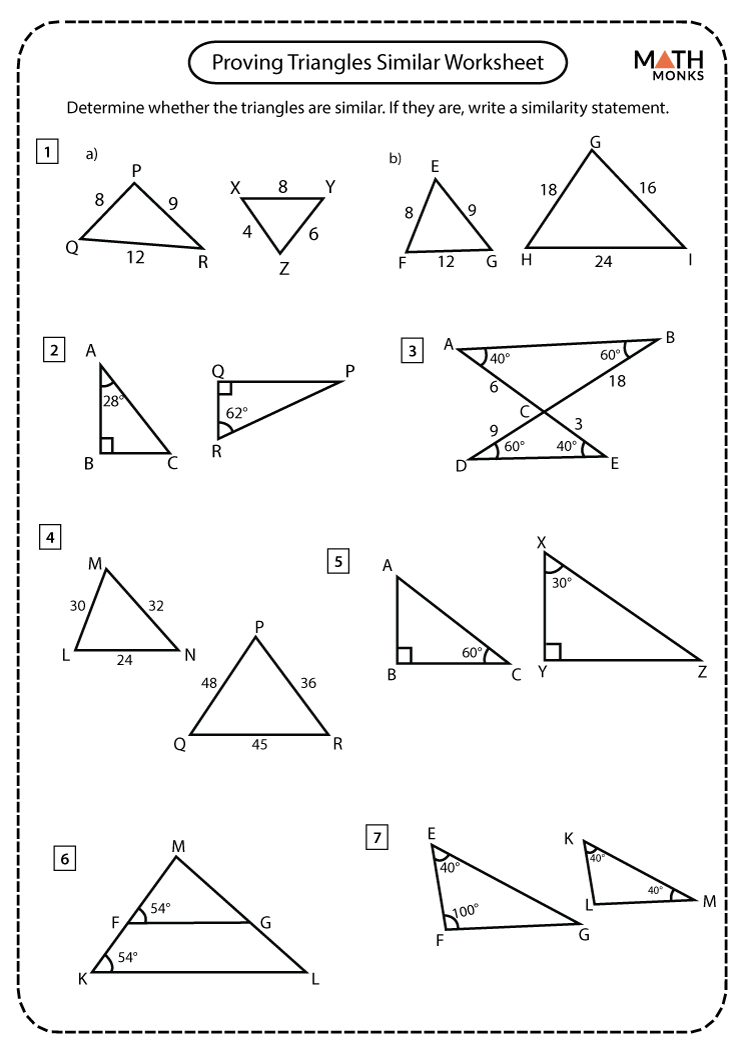
Graph Characteristics Worksheet Answers and Study Guide

Understanding Graph Characteristics: A Comprehensive Study Guide
Graphs are a fundamental concept in mathematics, representing relationships between variables in a visual format. Understanding the characteristics of graphs is essential for analyzing and interpreting data, making informed decisions, and solving problems. This study guide provides a detailed explanation of graph characteristics, including their definitions, examples, and importance.
Types of Graphs
Graphs can be broadly classified into several types, each with its unique characteristics.
- Linear Graphs: A linear graph is a graph that represents a linear relationship between two variables. It is characterized by a straight line.
- Non-Linear Graphs: A non-linear graph is a graph that represents a non-linear relationship between two variables. It is characterized by a curved line.
- Quadratic Graphs: A quadratic graph is a graph that represents a quadratic relationship between two variables. It is characterized by a parabolic shape.
- Exponential Graphs: An exponential graph is a graph that represents an exponential relationship between two variables. It is characterized by a rapid increase or decrease.
Graph Characteristics
Graphs have several characteristics that help us understand and analyze them. These characteristics include:
- X-Intercept: The x-intercept is the point where the graph intersects the x-axis. It is the value of x when y is equal to zero.
- Y-Intercept: The y-intercept is the point where the graph intersects the y-axis. It is the value of y when x is equal to zero.
- Slope: The slope of a graph is a measure of how steep it is. It is calculated by dividing the change in y by the change in x.
- Maxima and Minima: The maxima and minima of a graph are the highest and lowest points on the graph.
- Axes of Symmetry: The axes of symmetry are the lines that divide the graph into two symmetrical parts.
Graph Transformations
Graph transformations are changes made to the graph to shift, reflect, or stretch it. These transformations include:
- Translation: A translation is a shift of the graph in the x or y direction.
- Reflection: A reflection is a flip of the graph over the x or y axis.
- Dilation: A dilation is a stretch or shrink of the graph in the x or y direction.
Importance of Graph Characteristics
Understanding graph characteristics is essential in various fields, including:
- Science: Graphs are used to represent data in science, such as the relationship between temperature and time.
- Finance: Graphs are used to represent financial data, such as stock prices and trends.
- Engineering: Graphs are used to represent engineering data, such as stress and strain.
📝 Note: Graph characteristics are essential in problem-solving and decision-making. By understanding these characteristics, we can analyze and interpret data effectively.
Common Graphs and Their Characteristics

| Graph | Characteristics |
|---|---|
| Linear Graph | Straight line, constant slope |
| Quadratic Graph | Parabolic shape, maxima or minima |
| Exponential Graph | Rapid increase or decrease, asymptote |
| Sinusoidal Graph | Wavy shape, periodic |
Conclusion
In conclusion, graph characteristics are essential in understanding and analyzing data. By recognizing the types of graphs, characteristics, and transformations, we can effectively interpret and use data to make informed decisions. Remember, graph characteristics are the building blocks of data analysis, and mastering them will help you succeed in various fields.
What is the difference between a linear and non-linear graph?
+
A linear graph represents a linear relationship between two variables, while a non-linear graph represents a non-linear relationship. A linear graph has a straight line, while a non-linear graph has a curved line.
What is the importance of understanding graph characteristics?
+
Understanding graph characteristics is essential in problem-solving and decision-making. By recognizing graph characteristics, we can analyze and interpret data effectively, making informed decisions in various fields.
What is the difference between a maxima and minima?
+
A maxima is the highest point on the graph, while a minima is the lowest point on the graph. These points are essential in understanding the behavior of the graph.