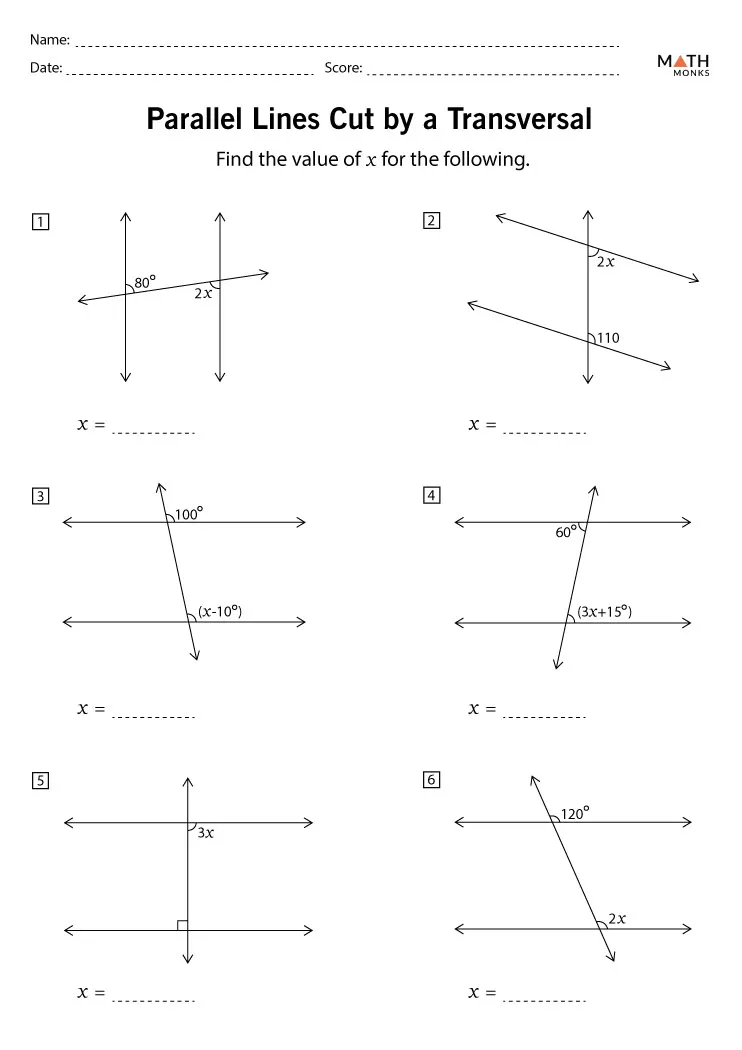
5 Easy Ways to Compare Fractions Using Benchmarks
Understanding Fractions and Benchmarks
When dealing with fractions, one of the most common challenges is comparing them to determine which one is larger or smaller. This is where benchmarks come in handy. Benchmarks are familiar fractions that serve as reference points, making it easier to compare and understand the relative size of other fractions. In this article, we will explore 5 easy ways to compare fractions using benchmarks, making it a breeze for students and individuals to grasp this concept.
Method 1: Using 1/2 as a Benchmark
One of the most useful benchmarks is 1⁄2. This fraction is easy to understand and can be used as a reference point to compare other fractions. When comparing fractions, ask yourself:
- Is the fraction greater than or less than 1⁄2?
- Is the fraction close to 1⁄2 or far away from it?
For example, let’s compare the fractions 3⁄4 and 2⁄3 using 1⁄2 as a benchmark.
- 3⁄4 is greater than 1⁄2 because 3 is greater than 2.
- 2⁄3 is also greater than 1⁄2, but not as great as 3⁄4.
Therefore, 3⁄4 is greater than 2⁄3.
Method 2: Using 1/4 as a Benchmark
Another useful benchmark is 1⁄4. This fraction is also easy to understand and can be used to compare fractions that are close to it.
- Is the fraction greater than or less than 1⁄4?
- Is the fraction close to 1⁄4 or far away from it?
For example, let’s compare the fractions 3⁄8 and 1⁄3 using 1⁄4 as a benchmark.
- 3⁄8 is greater than 1⁄4 because 3 is greater than 2.
- 1⁄3 is less than 1⁄4 because 1 is less than 2.
Therefore, 3⁄8 is greater than 1⁄3.
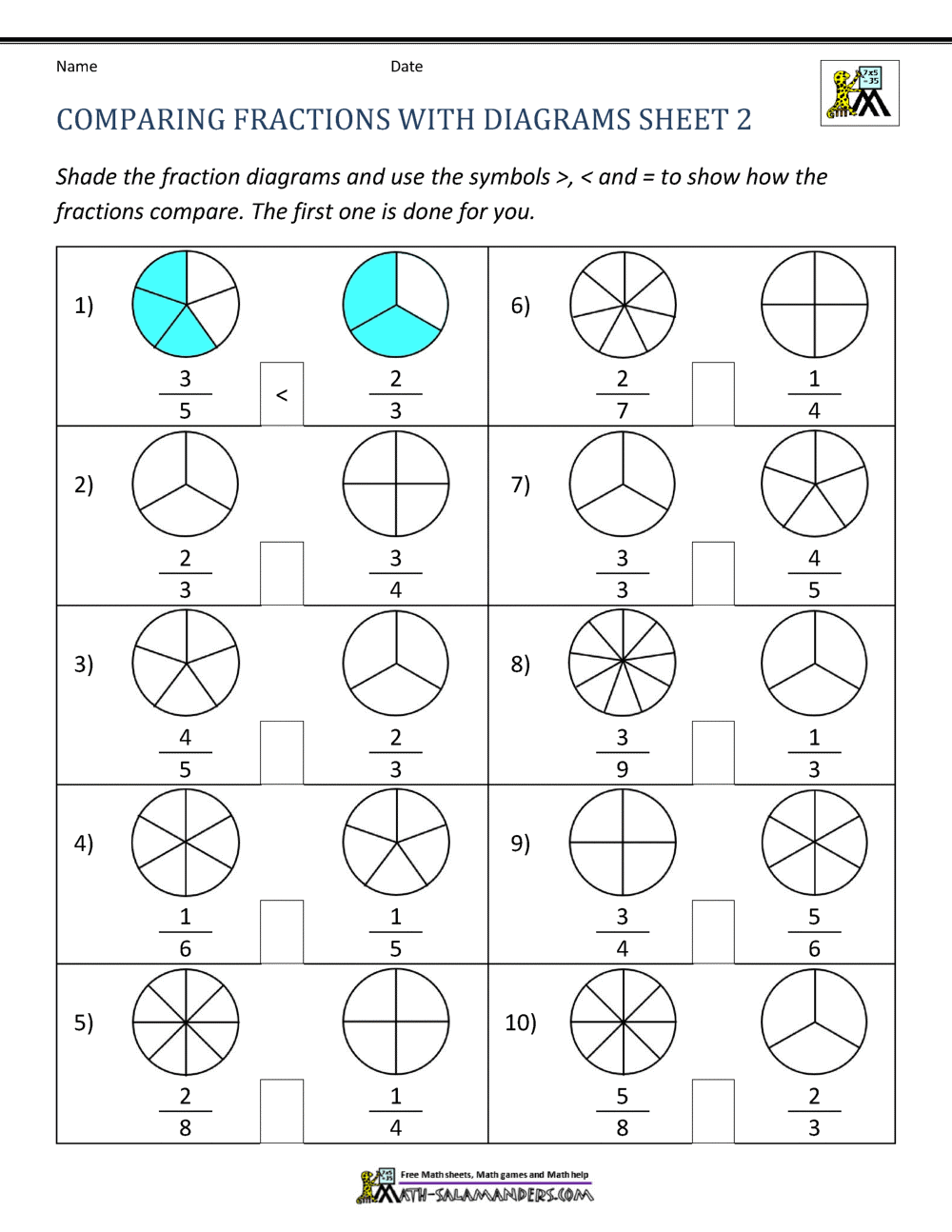
Method 3: Using Visual Models
Visual models are an excellent way to compare fractions. By drawing diagrams or using real-life objects, you can compare fractions and determine which one is larger or smaller.
For example, let’s compare the fractions 2⁄3 and 3⁄4 using a visual model.
- Draw a rectangle and divide it into 3 equal parts to represent 2⁄3.
- Draw another rectangle and divide it into 4 equal parts to represent 3⁄4.
By comparing the two diagrams, you can see that 3⁄4 is greater than 2⁄3.
📝 Note: Visual models are an excellent way to compare fractions, but they can be time-consuming to draw. Use them sparingly and only when necessary.
Method 4: Using Equivalent Fractions
Equivalent fractions are fractions that have the same value but different numerators and denominators. By converting fractions to equivalent fractions, you can compare them easily.
For example, let’s compare the fractions 2⁄3 and 3⁄4 by converting them to equivalent fractions.
- 2⁄3 = 8⁄12
- 3⁄4 = 9⁄12
By comparing the equivalent fractions, you can see that 3⁄4 is greater than 2⁄3.
Method 5: Using a Number Line
A number line is a visual representation of numbers on a line. By placing fractions on a number line, you can compare them easily.
For example, let’s compare the fractions 1⁄2 and 3⁄4 using a number line.
- Place 1⁄2 on the number line at 0.5.
- Place 3⁄4 on the number line at 0.75.
By comparing the two fractions on the number line, you can see that 3⁄4 is greater than 1⁄2.
| Fraction | Number Line Representation |
|---|---|
| 1/2 | 0.5 |
| 3/4 | 0.75 |
In conclusion, comparing fractions using benchmarks is an easy and effective way to understand their relative size. By using the 5 methods outlined in this article, you can compare fractions with ease and confidence. Whether you’re a student or an individual looking to improve your math skills, these methods will help you master the art of comparing fractions.
What is a benchmark in math?
+A benchmark is a familiar fraction that serves as a reference point to compare other fractions.
How do I compare fractions using benchmarks?
+You can compare fractions using benchmarks by asking yourself if the fraction is greater than or less than the benchmark, and if it’s close to or far away from it.
What are some common benchmarks used to compare fractions?
+Some common benchmarks used to compare fractions include 1⁄2, 1⁄4, and 3⁄4.
Related Terms:
- Teacher synergy llc
- IXL
- Khan Academy
- BrainPOP
- Udacity
- Duolingo