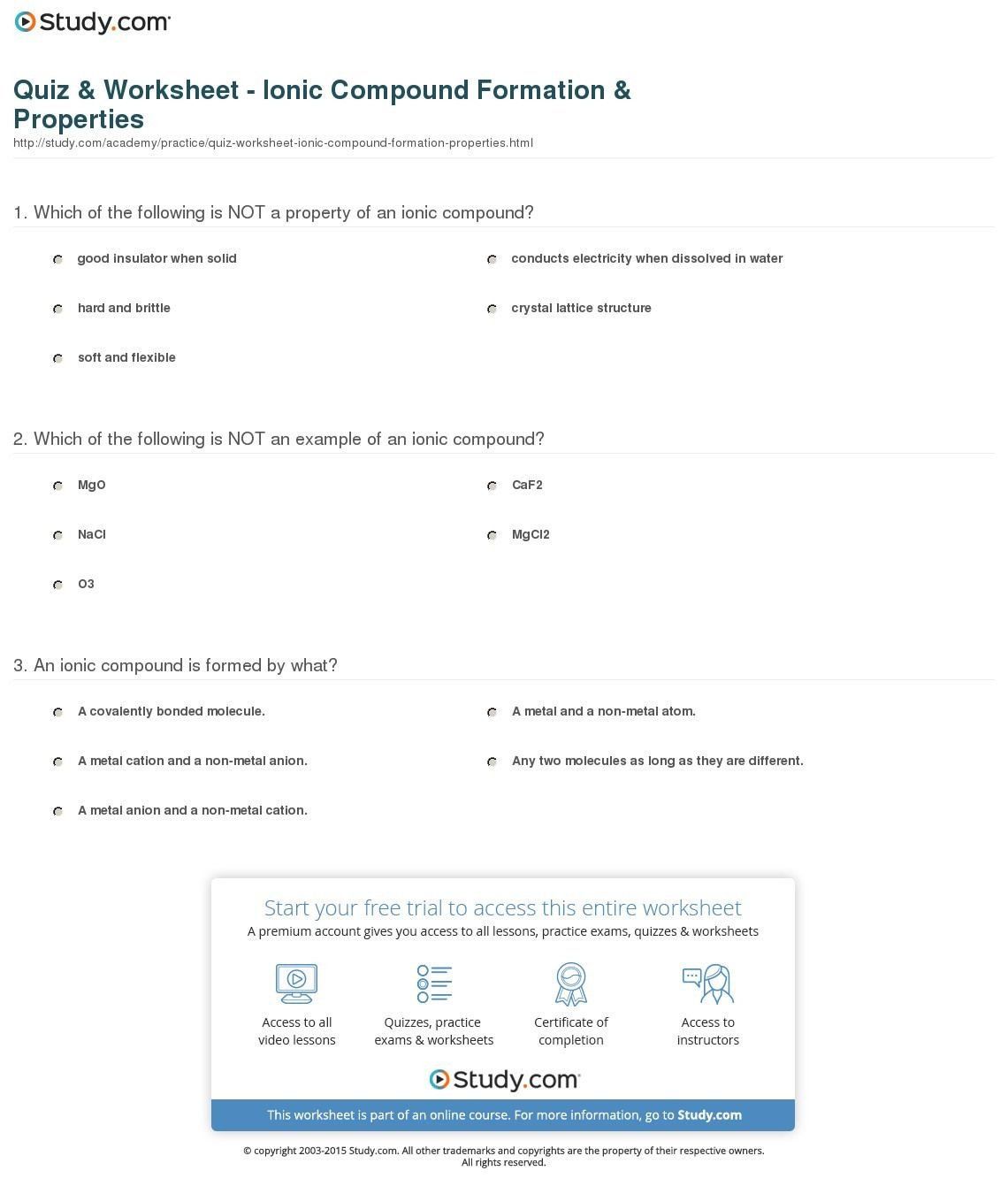
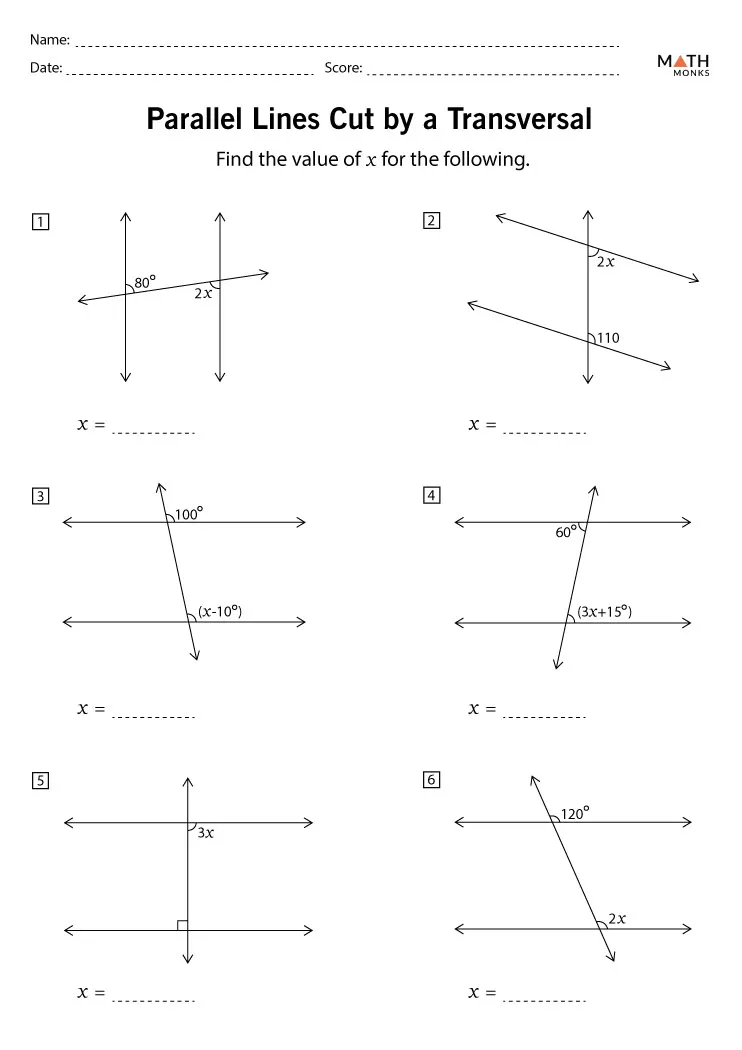
Parallel Lines Cut by a Transversal Practice Worksheet
Understanding Parallel Lines Cut by a Transversal
Parallel lines are lines that lie in the same plane and never intersect, no matter how far they are extended. When a transversal line intersects two parallel lines, it creates several angles that have special properties. In this article, we will explore the concept of parallel lines cut by a transversal and provide a practice worksheet to help you master this topic.
Key Concepts and Theorems
When a transversal line intersects two parallel lines, it creates several types of angles, including:
- Corresponding Angles: Angles that are in the same relative position in each of the parallel lines.
- Alternate Interior Angles: Angles that are on opposite sides of the transversal and inside the parallel lines.
- Alternate Exterior Angles: Angles that are on opposite sides of the transversal and outside the parallel lines.
- Interior Angles on the Same Side of the Transversal: Angles that are on the same side of the transversal and inside the parallel lines.
The following theorems are essential to understanding parallel lines cut by a transversal:
- Corresponding Angles Theorem: If two parallel lines are cut by a transversal, then the corresponding angles are congruent.
- Alternate Interior Angles Theorem: If two parallel lines are cut by a transversal, then the alternate interior angles are congruent.
- Alternate Exterior Angles Theorem: If two parallel lines are cut by a transversal, then the alternate exterior angles are congruent.
- Interior Angles on the Same Side of the Transversal Theorem: If two parallel lines are cut by a transversal, then the interior angles on the same side of the transversal are supplementary.
Practice Worksheet
Section 1: Multiple Choice Questions
- If two parallel lines are cut by a transversal, what can be concluded about the corresponding angles? a) They are supplementary b) They are complementary c) They are congruent d) They are not related
Answer: c) They are congruent
- If two parallel lines are cut by a transversal, what can be concluded about the alternate interior angles? a) They are supplementary b) They are complementary c) They are congruent d) They are not related
Answer: c) They are congruent
- If two parallel lines are cut by a transversal, what can be concluded about the interior angles on the same side of the transversal? a) They are supplementary b) They are complementary c) They are congruent d) They are not related
Answer: a) They are supplementary
Section 2: Short Answer Questions
- In the diagram below, line AB is parallel to line CD, and line EF is a transversal. Find the measure of angle 1.
Answer: _______________________
- In the diagram below, line GH is parallel to line IJ, and line KL is a transversal. Find the measure of angle 2.
Answer: _______________________
Section 3: Problems
- In the diagram below, line AB is parallel to line CD, and line EF is a transversal. If angle 1 measures 60°, find the measure of angle 2.
Answer: _______________________
- In the diagram below, line GH is parallel to line IJ, and line KL is a transversal. If angle 1 measures 30°, find the measure of angle 2.
Answer: _______________________
Notes
📝 Note: When solving problems involving parallel lines cut by a transversal, make sure to identify the corresponding angles, alternate interior angles, alternate exterior angles, and interior angles on the same side of the transversal.
📝 Note: Use the theorems and properties of parallel lines cut by a transversal to find the measures of the angles.
Review and Practice
To master the concept of parallel lines cut by a transversal, review the key concepts and theorems, and practice solving problems. Start with simple problems and gradually move on to more complex ones. Use the practice worksheet provided above to test your understanding and skills.
What is a transversal?
+A transversal is a line that intersects two or more other lines.
What are corresponding angles?
+Corresponding angles are angles that are in the same relative position in each of the parallel lines.
What is the alternate interior angles theorem?
+The alternate interior angles theorem states that if two parallel lines are cut by a transversal, then the alternate interior angles are congruent.
To summarize, parallel lines cut by a transversal create several types of angles with special properties. Understanding the corresponding angles theorem, alternate interior angles theorem, alternate exterior angles theorem, and interior angles on the same side of the transversal theorem is essential to solving problems involving parallel lines cut by a transversal. By reviewing the key concepts and practicing problems, you can master this topic and become proficient in geometry.
Related Terms:
- teacher synergy llc
- Khan Academy
- IXL
- BrainPOP
- Udacity
- Duolingo