Domain and Range Graph Worksheet Answers
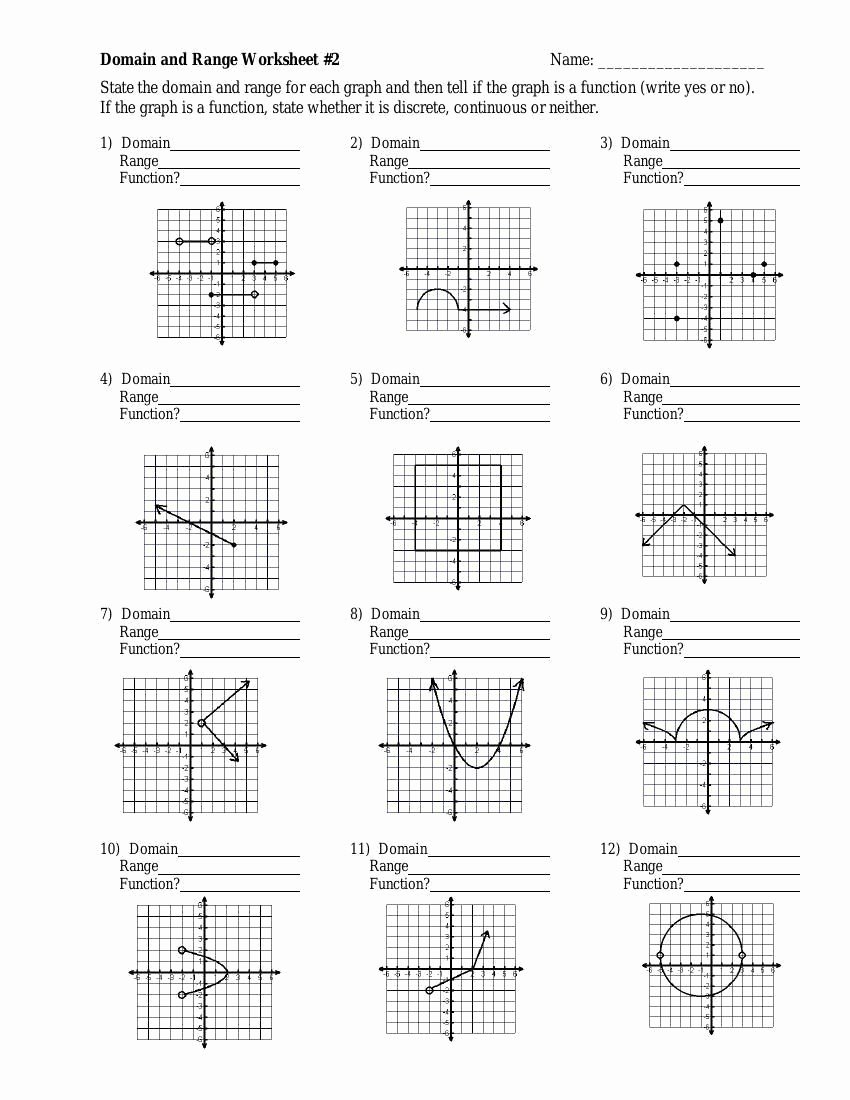
Understanding the domain and range of a function is crucial in mathematics, particularly in algebra and calculus. This worksheet will guide you through understanding the domain and range of various functions, including linear, quadratic, and rational functions.
Linear Functions
A linear function is a function whose graph is a straight line. The domain of a linear function is all real numbers, unless the function is a constant function, in which case the domain is a single point.
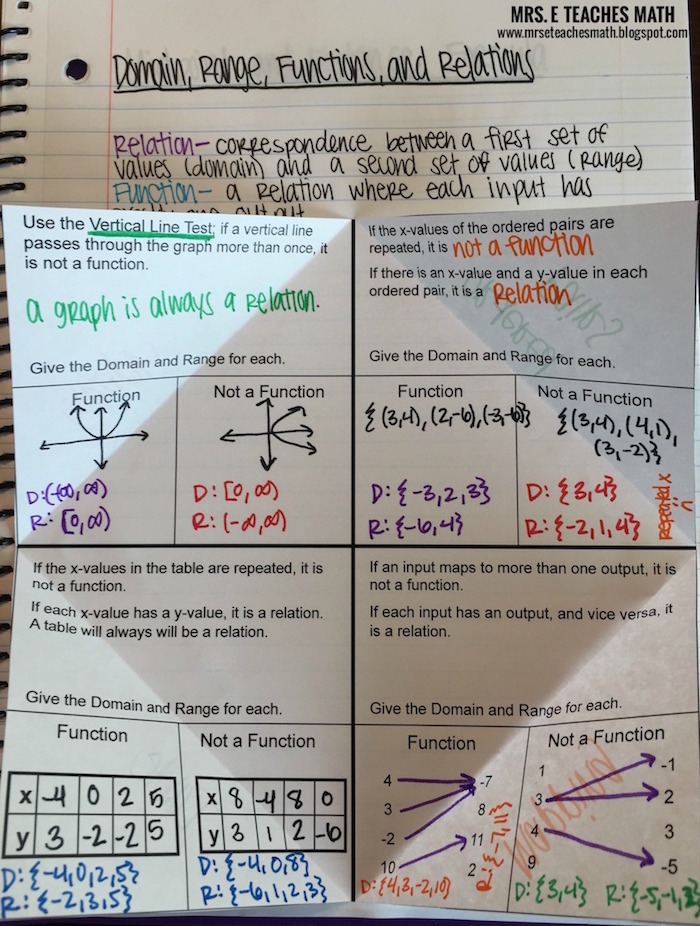
| Function | Domain | Range |
|---|---|---|
| f(x) = 2x + 1 | All real numbers | All real numbers |
| f(x) = x - 3 | All real numbers | All real numbers |
| f(x) = 4 | {4} | {4} |
Quadratic Functions
A quadratic function is a function of the form f(x) = ax^2 + bx + c, where a, b, and c are constants. The domain of a quadratic function is all real numbers.
| Function | Domain | Range |
|---|---|---|
| f(x) = x^2 + 2x + 1 | All real numbers | [1, ∞) |
| f(x) = -x^2 + 3x - 2 | All real numbers | (-∞, 5⁄4] |
| f(x) = x^2 - 4 | All real numbers | [-4, ∞) |
Rational Functions
A rational function is a function of the form f(x) = p(x)/q(x), where p(x) and q(x) are polynomials. The domain of a rational function consists of all real numbers except those for which the denominator is zero.
| Function | Domain | Range |
|---|---|---|
| f(x) = 1/x | All real numbers except x = 0 | All real numbers except y = 0 |
| f(x) = (x + 1)/(x - 2) | All real numbers except x = 2 | All real numbers except y = 1 |
| f(x) = x/(x^2 + 1) | All real numbers | (-1⁄2, 1⁄2) |
Notes
- The domain of a function is the set of all input values for which the function is defined.
- The range of a function is the set of all possible output values.
- The graph of a function can help determine the domain and range of the function.
- The domain and range of a function can be affected by the presence of asymptotes, holes, and other graph features.
Table of Domain and Range Notations
| Notation | Meaning |
|---|---|
| (-∞, ∞) | All real numbers |
| [a, b] | All real numbers from a to b, including a and b |
| (a, b) | All real numbers from a to b, excluding a and b |
| (a, ∞) | All real numbers greater than a |
| (-∞, b) | All real numbers less than b |
Example 1
Find the domain and range of the function f(x) = 1/(x - 1).
The domain of the function is all real numbers except x = 1, since the denominator cannot be zero. Therefore, the domain is (-∞, 1) ∪ (1, ∞).
To find the range, we can analyze the behavior of the function. As x approaches 1 from the left, the function values approach negative infinity. As x approaches 1 from the right, the function values approach positive infinity. Therefore, the range is all real numbers except y = 0.
Example 2
Find the domain and range of the function f(x) = x^2 - 4.
The domain of the function is all real numbers, since the function is defined for all input values.
To find the range, we can analyze the behavior of the function. The minimum value of the function occurs at x = 0, where f(x) = -4. The function values increase without bound as x moves away from 0. Therefore, the range is [-4, ∞).
In conclusion, understanding the domain and range of a function is essential in mathematics. The domain and range can be affected by the presence of asymptotes, holes, and other graph features. By analyzing the behavior of the function, we can determine the domain and range of the function.
Related Terms:
- Domain and Range Worksheet 2