6 Ways to Master Composite Figures Worksheets

Unlocking the Secrets of Composite Figures Worksheets

Composite figures worksheets are a staple in many math classrooms, providing students with a fun and engaging way to practice their geometry skills. However, these worksheets can also be a source of frustration for some students, especially those who struggle with visualizing and breaking down complex shapes. In this article, we’ll explore six ways to master composite figures worksheets, making it easier for you to help your students succeed.

What are Composite Figures?

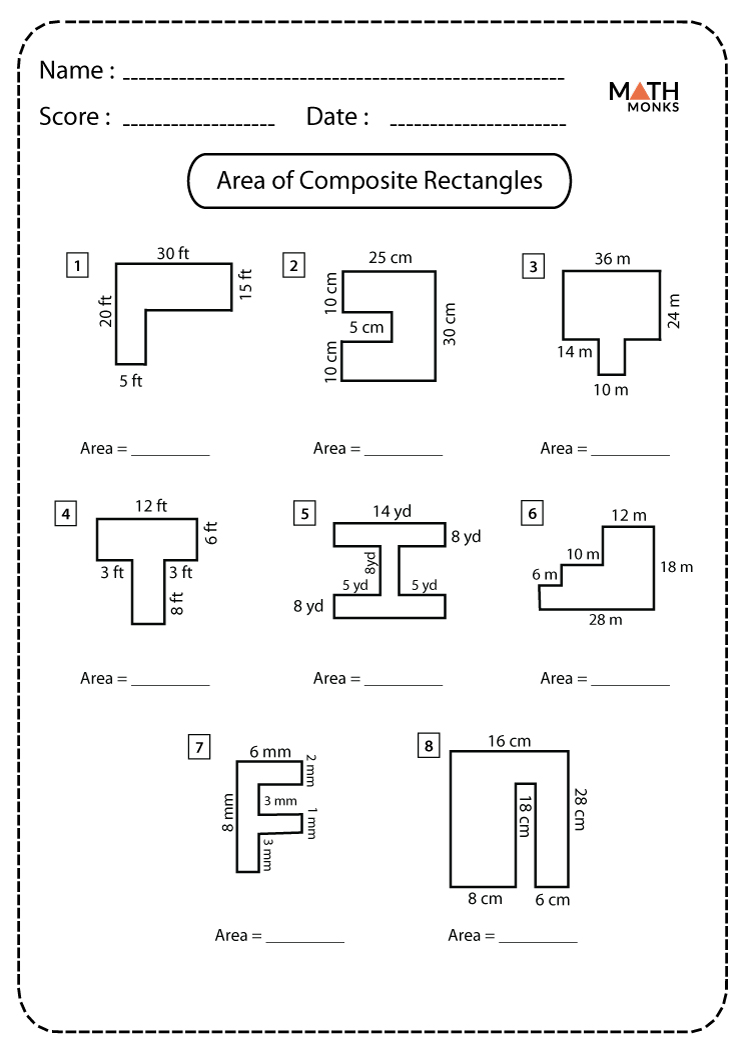
Before diving into the strategies, let’s quickly review what composite figures are. Composite figures are shapes made up of two or more simpler shapes, such as triangles, rectangles, and circles. These figures can be combined in various ways, creating unique and challenging shapes for students to work with.

1. Break Down the Shape

One of the most effective ways to approach composite figures worksheets is to break down the shape into its individual components. Encourage your students to identify the simpler shapes within the composite figure and label each one. This will help them visualize the shape and make it easier to calculate the area, perimeter, or other required measurements.

📝 Note: Emphasize the importance of labeling each shape correctly, as this will help students keep track of their calculations.

2. Use Visual Aids

Visual aids can be a powerful tool when working with composite figures. Consider using diagrams, charts, or graphs to help students visualize the shape and its components. You can also use real-world examples, such as architecture or design, to illustrate how composite figures are used in everyday life.

3. Practice with Simple Shapes

Before diving into complex composite figures, make sure your students are comfortable working with simple shapes. Provide them with worksheets that focus on basic shapes, such as triangles, rectangles, and circles. This will help build their confidence and skills, making it easier to tackle more complex composite figures.

4. Focus on Area and Perimeter

When working with composite figures, it’s essential to focus on calculating the area and perimeter of each individual shape. This will help students develop a deeper understanding of the shape’s properties and make it easier to calculate the overall area and perimeter of the composite figure.

5. Use Formulas and Theorems

Composite figures often require the use of formulas and theorems, such as the formula for the area of a triangle (A = 0.5bh) or the Pythagorean theorem (a^2 + b^2 = c^2). Make sure your students are familiar with these formulas and theorems, and encourage them to use them when working with composite figures.

6. Encourage Problem-Solving

Finally, encourage your students to approach composite figures worksheets as problem-solving exercises. Encourage them to think creatively and critically, using their knowledge of geometry and measurement to solve complex problems.

By following these six strategies, your students will be well on their way to mastering composite figures worksheets. Remember to provide plenty of practice opportunities and encourage students to think creatively and critically.

Here’s a summary of the key points:

• Break down the shape into its individual components
• Use visual aids to help students visualize the shape
• Practice with simple shapes before moving on to complex composite figures
• Focus on calculating the area and perimeter of each individual shape
• Use formulas and theorems to solve problems
• Encourage problem-solving and critical thinking