7 Ways to Master Angles Formed by Transversals
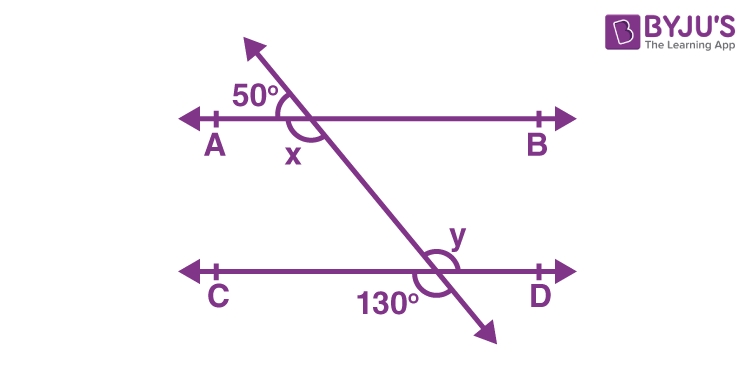
Unlocking the Secrets of Angles Formed by Transversals
Angles formed by transversals are a fundamental concept in geometry, and mastering them is essential for problem-solving and critical thinking. A transversal is a line that intersects two or more other lines, and the angles formed by these intersections can be complex and challenging to understand. However, with practice and persistence, you can become proficient in working with angles formed by transversals. In this article, we will explore seven ways to master angles formed by transversals.
Understanding the Basics
Before diving into the world of angles formed by transversals, it’s essential to understand the basic concepts of angles and lines. An angle is formed by two rays sharing a common endpoint, and it can be measured in degrees. A transversal is a line that intersects two or more other lines, and it can form various types of angles, including corresponding angles, alternate interior angles, and alternate exterior angles.
1. Identifying Angle Relationships
The first step to mastering angles formed by transversals is to identify the different types of angle relationships. These relationships include:
- Corresponding Angles: Angles that are in the same position relative to the transversal and the intersected lines.
- Alternate Interior Angles: Angles that are on opposite sides of the transversal and inside the intersected lines.
- Alternate Exterior Angles: Angles that are on opposite sides of the transversal and outside the intersected lines.
- Interior Angles: Angles that are inside the intersected lines and on the same side of the transversal.
- Exterior Angles: Angles that are outside the intersected lines and on the same side of the transversal.
📝 Note: Understanding these angle relationships is crucial for problem-solving and critical thinking.
2. Using Properties of Angles Formed by Transversals
Angles formed by transversals have several properties that can be used to solve problems. These properties include:
- Corresponding Angles are Congruent: Corresponding angles formed by a transversal are equal in measure.
- Alternate Interior Angles are Congruent: Alternate interior angles formed by a transversal are equal in measure.
- Alternate Exterior Angles are Congruent: Alternate exterior angles formed by a transversal are equal in measure.
- Interior Angles on the Same Side of the Transversal are Supplementary: Interior angles on the same side of the transversal add up to 180 degrees.
📝 Note: These properties can be used to solve problems involving angles formed by transversals.
3. Solving Problems Involving Angles Formed by Transversals
Solving problems involving angles formed by transversals requires critical thinking and problem-solving skills. Here are some steps to follow:
- Read the Problem Carefully: Read the problem carefully and identify the given information and the unknown quantities.
- Draw a Diagram: Draw a diagram to visualize the problem and identify the angles formed by the transversal.
- Use Properties of Angles Formed by Transversals: Use the properties of angles formed by transversals to solve the problem.
4. Working with Transversals and Parallel Lines
Transversals and parallel lines are closely related, and understanding this relationship is essential for mastering angles formed by transversals. When a transversal intersects two parallel lines, the following properties hold:
- Corresponding Angles are Congruent: Corresponding angles formed by a transversal and two parallel lines are equal in measure.
- Alternate Interior Angles are Congruent: Alternate interior angles formed by a transversal and two parallel lines are equal in measure.
- Alternate Exterior Angles are Congruent: Alternate exterior angles formed by a transversal and two parallel lines are equal in measure.
5. Using Angle Sum Properties
Angle sum properties can be used to solve problems involving angles formed by transversals. Here are some angle sum properties:
- Interior Angles on the Same Side of the Transversal add up to 180 Degrees: Interior angles on the same side of the transversal add up to 180 degrees.
- Exterior Angles on the Same Side of the Transversal add up to 360 Degrees: Exterior angles on the same side of the transversal add up to 360 degrees.
6. Identifying Similar Triangles
Similar triangles can be used to solve problems involving angles formed by transversals. When two triangles are similar, their corresponding angles are equal, and their corresponding sides are proportional.
7. Practicing with Real-World Applications
Finally, practicing with real-world applications is essential for mastering angles formed by transversals. Here are some real-world applications:
- Architecture: Angles formed by transversals are used in architecture to design buildings and bridges.
- Engineering: Angles formed by transversals are used in engineering to design mechanical systems and electrical circuits.
- Physics: Angles formed by transversals are used in physics to describe the motion of objects.
In conclusion, mastering angles formed by transversals requires practice, persistence, and critical thinking. By understanding the basics, identifying angle relationships, using properties of angles formed by transversals, solving problems, working with transversals and parallel lines, using angle sum properties, identifying similar triangles, and practicing with real-world applications, you can become proficient in working with angles formed by transversals.
What is a transversal?
+A transversal is a line that intersects two or more other lines.
What are the different types of angle relationships formed by a transversal?
+The different types of angle relationships formed by a transversal include corresponding angles, alternate interior angles, alternate exterior angles, interior angles, and exterior angles.
What is the relationship between transversals and parallel lines?
+When a transversal intersects two parallel lines, the corresponding angles, alternate interior angles, and alternate exterior angles are congruent.



