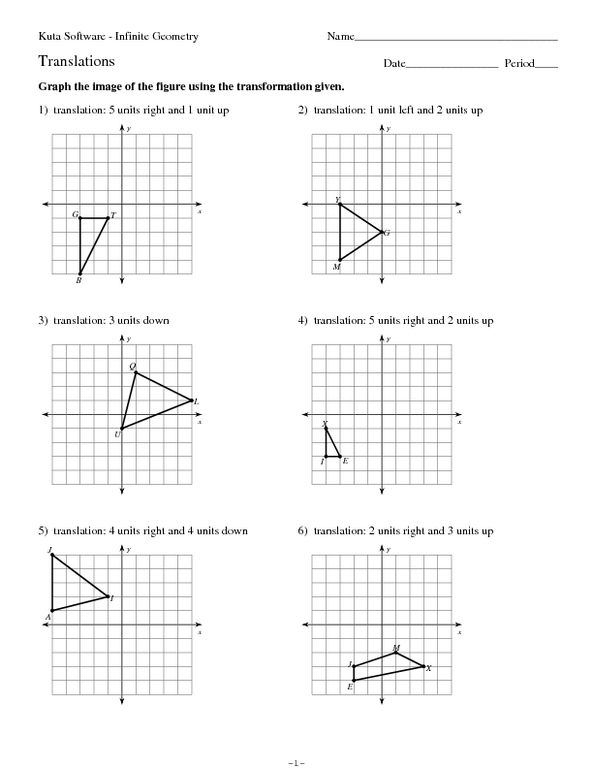
5 Easy Ways to Master Scientific Notation

Understanding Scientific Notation
Scientific notation is a shorthand way of writing very large or very small numbers. It’s commonly used in science, engineering, and mathematics to simplify complex calculations and make them more manageable. In this article, we’ll explore five easy ways to master scientific notation, making it a breeze to work with even the most daunting numbers.
What is Scientific Notation?
Scientific notation is a way of expressing numbers in the form of a number between 1 and 10, multiplied by a power of 10. For example, the number 456,000,000 can be written in scientific notation as 4.56 × 10^8. This notation makes it easy to perform calculations and comparisons without having to deal with cumbersome digits.
Method 1: Convert to Scientific Notation
To convert a number to scientific notation, follow these steps:
- Move the decimal point to the left or right until you have a number between 1 and 10.
- Count the number of places you moved the decimal point.
- Write the number as a coefficient (the number between 1 and 10) multiplied by 10 raised to the power of the number of places you moved the decimal point.
For example, let’s convert the number 456,000,000 to scientific notation:
- Move the decimal point 8 places to the left to get 4.56.
- Count the number of places: 8.
- Write the number as 4.56 × 10^8.
📝 Note: When moving the decimal point to the left, the exponent will be positive. When moving it to the right, the exponent will be negative.
Method 2: Multiply and Divide in Scientific Notation
When multiplying or dividing numbers in scientific notation, follow these rules:
- Multiply the coefficients (the numbers between 1 and 10).
- Add or subtract the exponents (the powers of 10).
For example, let’s multiply 4.56 × 10^8 and 2.34 × 10^5:
- Multiply the coefficients: 4.56 × 2.34 = 10.66.
- Add the exponents: 10^8 + 10^5 = 10^13.
- Write the result as 10.66 × 10^13.
To divide, follow the same rules, but subtract the exponents instead of adding them.
Method 3: Add and Subtract in Scientific Notation
When adding or subtracting numbers in scientific notation, follow these rules:
- Make sure the exponents are the same.
- Add or subtract the coefficients (the numbers between 1 and 10).
- Keep the same exponent.
For example, let’s add 4.56 × 10^8 and 2.34 × 10^8:
- Make sure the exponents are the same: 10^8.
- Add the coefficients: 4.56 + 2.34 = 6.90.
- Write the result as 6.90 × 10^8.
Method 4: Use Scientific Notation to Compare Numbers
Scientific notation makes it easy to compare numbers by comparing their coefficients and exponents. For example, let’s compare 4.56 × 10^8 and 2.34 × 10^5:
- Compare the coefficients: 4.56 is greater than 2.34.
- Compare the exponents: 10^8 is greater than 10^5.
- Therefore, 4.56 × 10^8 is greater than 2.34 × 10^5.
Method 5: Practice, Practice, Practice!
The best way to master scientific notation is to practice, practice, practice! Try converting numbers to scientific notation, multiplying and dividing numbers in scientific notation, and comparing numbers using scientific notation.

| Number | Scientific Notation |
|---|---|
| 456,000,000 | 4.56 × 10^8 |
| 234,000 | 2.34 × 10^5 |
| 0.000456 | 4.56 × 10^-4 |
By following these five easy methods, you’ll become a master of scientific notation in no time!
As you’ve learned, scientific notation is a powerful tool for simplifying complex calculations and comparing numbers. With practice, you’ll be able to work with even the most daunting numbers with ease.
What is the purpose of scientific notation?
+Scientific notation is used to simplify complex calculations and make them more manageable. It’s commonly used in science, engineering, and mathematics to express very large or very small numbers.
How do I convert a number to scientific notation?
+To convert a number to scientific notation, move the decimal point to the left or right until you have a number between 1 and 10, and then count the number of places you moved the decimal point. Write the number as a coefficient (the number between 1 and 10) multiplied by 10 raised to the power of the number of places you moved the decimal point.
How do I multiply and divide numbers in scientific notation?
+When multiplying or dividing numbers in scientific notation, multiply the coefficients (the numbers between 1 and 10), and add or subtract the exponents (the powers of 10).