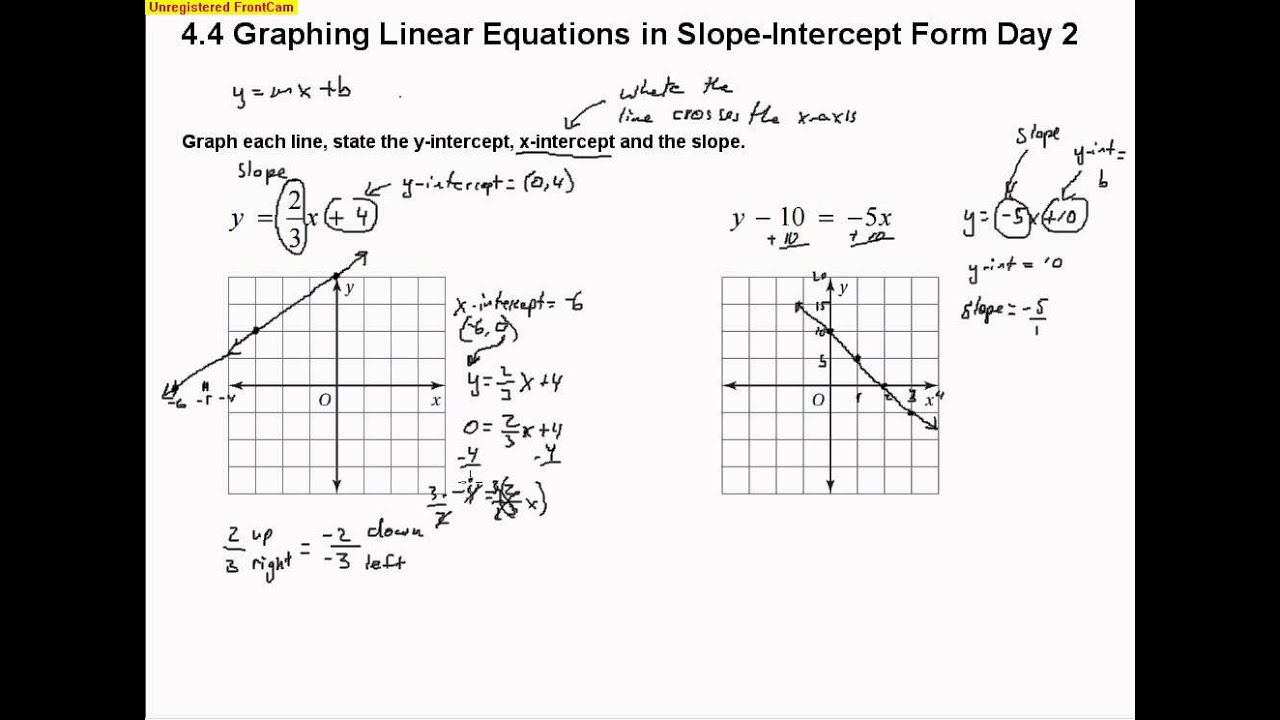
5 Ways to Find Slope of a Line

Understanding the Concept of Slope
The slope of a line is a fundamental concept in mathematics, particularly in algebra and geometry. It is a measure of how steep a line is and can be described as the ratio of the vertical change (rise) to the horizontal change (run) between two points on the line. The slope is denoted by the letter ’m’ and is calculated as the change in y-coordinates divided by the change in x-coordinates.
Why is Slope Important?
Slope is a crucial concept in various real-world applications, such as:
- Physics: to describe the steepness of a ramp or the rate of change of an object’s velocity
- Engineering: to design roads, bridges, and buildings
- Economics: to model the relationship between variables, such as cost and quantity
- Computer Science: to develop algorithms for image and signal processing
5 Ways to Find Slope of a Line
There are several ways to find the slope of a line, and the method you choose depends on the information given and your personal preference. Here are five common methods:
1. Using the Slope Formula
The slope formula is the most straightforward method to find the slope of a line. It is calculated as:
m = (y2 - y1) / (x2 - x1)
where (x1, y1) and (x2, y2) are two points on the line.
📝 Note: Make sure to subtract the y-coordinates and x-coordinates separately to avoid errors.
2. Using the Graph of the Line
If you have a graph of the line, you can find the slope by identifying two points on the line and using the slope formula. Alternatively, you can use the graph to estimate the slope by drawing a right triangle with the line as the hypotenuse.
3. Using the Equation of the Line
If you have the equation of the line in slope-intercept form (y = mx + b), the slope is simply the coefficient of x, which is ’m’.
For example, in the equation y = 2x + 3, the slope is 2.
4. Using Two Points on the Line
If you have two points on the line, you can find the slope by using the slope formula or by drawing a right triangle with the line as the hypotenuse.
5. Using the Perpendicular Distance from a Point to the Line
This method is useful when you have a point not on the line and want to find the slope of the line. You can draw a perpendicular line from the point to the line and use the slope formula to find the slope of the line.
| Method | Description |
|---|---|
| 1. Using the Slope Formula | Calculates the slope using two points on the line |
| 2. Using the Graph of the Line | Uses the graph to estimate the slope or identifies two points on the line |
| 3. Using the Equation of the Line | Finds the slope from the equation in slope-intercept form |
| 4. Using Two Points on the Line | Calculates the slope using two points on the line or draws a right triangle |
| 5. Using the Perpendicular Distance from a Point to the Line | Finds the slope using a perpendicular line from a point not on the line |
In conclusion, finding the slope of a line is an essential skill in mathematics and has numerous real-world applications. The five methods described above provide a comprehensive approach to finding the slope of a line, and the choice of method depends on the given information and personal preference. By mastering these methods, you can become proficient in calculating slopes and solving problems in various fields.
What is the slope formula?
+The slope formula is m = (y2 - y1) / (x2 - x1), where (x1, y1) and (x2, y2) are two points on the line.
What is the slope-intercept form of a line?
+The slope-intercept form of a line is y = mx + b, where ’m’ is the slope and ‘b’ is the y-intercept.
How do I find the slope of a line using the graph?
+You can find the slope of a line using the graph by identifying two points on the line and using the slope formula or by drawing a right triangle with the line as the hypotenuse.
Related Terms:
- Finding Slope Worksheet PDF
- Slope worksheets 8th grade PDF