5 Ways to Factor by Grouping

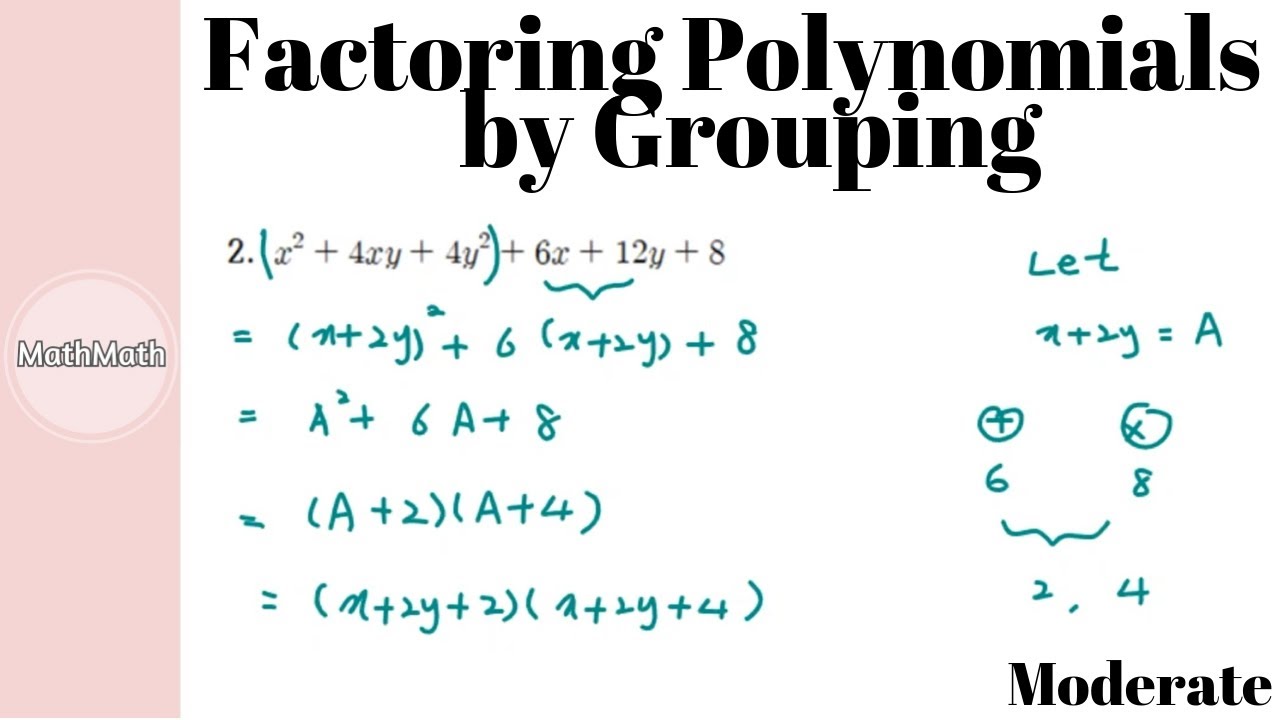
Understanding Factoring by Grouping

Factoring by grouping is a method used to factorize algebraic expressions that cannot be easily factored using simple techniques like finding the greatest common factor (GCF) or recognizing the difference of squares. This method involves grouping terms in a way that allows us to extract common factors from each group, making it easier to factorize the expression. In this blog post, we will explore five ways to factor by grouping and provide examples to illustrate each method.

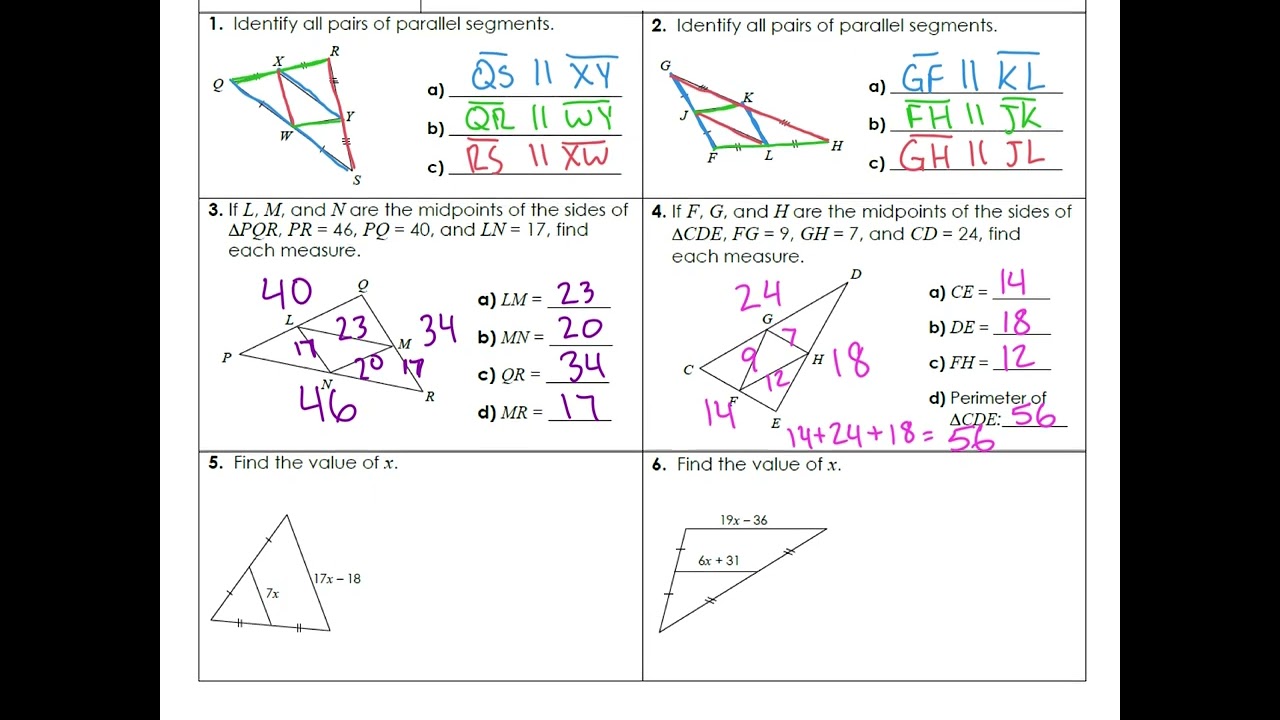
Method 1: Factoring by Grouping in Quadratic Expressions

This method involves factoring a quadratic expression by grouping the terms in such a way that we can extract a common factor from each group. Let’s consider the following example:

📝 Note: This method is particularly useful when the quadratic expression cannot be easily factored using other methods.

Example: Factor the quadratic expression x^2 + 5x + 6

Solution: We can group the terms as follows: (x^2 + 5x) + 6

By factoring out the GCF from each group, we get: x(x + 5) + 6

We can then rewrite the expression as: x(x + 5) + 2(x + 5)

Now, we can factor out the common binomial factor (x + 5): (x + 2)(x + 5)

Method 2: Factoring by Grouping in Cubic Expressions

This method involves factoring a cubic expression by grouping the terms in such a way that we can extract a common factor from each group. Let’s consider the following example:

Example: Factor the cubic expression x^3 + 2x^2 + 3x + 6

Solution: We can group the terms as follows: (x^3 + 2x^2) + (3x + 6)

By factoring out the GCF from each group, we get: x^2(x + 2) + 3(x + 2)

We can then rewrite the expression as: (x^2 + 3)(x + 2)

Method 3: Factoring by Grouping with Coefficients

This method involves factoring an expression by grouping the terms in such a way that we can extract a common factor from each group, taking into account the coefficients. Let’s consider the following example:

Example: Factor the expression 2x^2 + 6x + 5x + 15

Solution: We can group the terms as follows: (2x^2 + 6x) + (5x + 15)

By factoring out the GCF from each group, we get: 2x(x + 3) + 5(x + 3)

We can then rewrite the expression as: (2x + 5)(x + 3)

Method 4: Factoring by Grouping with Negative Coefficients

This method involves factoring an expression by grouping the terms in such a way that we can extract a common factor from each group, taking into account the negative coefficients. Let’s consider the following example:

Example: Factor the expression -2x^2 - 6x + 5x + 15

Solution: We can group the terms as follows: (-2x^2 - 6x) + (5x + 15)

By factoring out the GCF from each group, we get: -2x(x + 3) + 5(x + 3)

We can then rewrite the expression as: (5 - 2x)(x + 3)

Method 5: Factoring by Grouping with Complex Expressions

This method involves factoring a complex expression by grouping the terms in such a way that we can extract a common factor from each group. Let’s consider the following example:

Example: Factor the expression x^4 + 2x^3 + 3x^2 + 6x + 2

Solution: We can group the terms as follows: (x^4 + 2x^3) + (3x^2 + 6x) + 2

By factoring out the GCF from each group, we get: x^3(x + 2) + 3x(x + 2) + 2

We can then rewrite the expression as: (x^3 + 3x + 2)(x + 2)

📝 Note: Factoring by grouping can be a challenging method, and it requires practice to become proficient.

In conclusion, factoring by grouping is a powerful method for factoring algebraic expressions. By grouping terms in a way that allows us to extract common factors from each group, we can factorize expressions that cannot be easily factored using other methods. The five methods presented in this blog post provide a comprehensive overview of factoring by grouping, and with practice, you can become proficient in using this method to factor a wide range of algebraic expressions.

Related Terms:

• Factoring by grouping worksheet corbettmaths
• Factoring by grouping Worksheet easy
• How to factor by grouping